Description：

给定正整数 $n$ 和正整数序列 $A$ ， $|A|=2^{n-1}$ 。对于每一个 $k(1\leqslant k<2^n)$ ，输出满足 $i\text{ or }j\leqslant k$ 的最大 $a_i+a_J$ 值。

$1\leqslant n\leqslant 18$

Solution：

先变化一下条件，对每个 $k$ 求出 $i\text{ or }j=k$ 的最大的 $a_i+a_j$ 的值，放宽一下约束条件，可以看成 $i\in k$ 的 $a_i$ 的最大值和次大值，这样一定合法且不会丢解，那发现这就是一个子集统计问题，可以用快速莫比乌斯变换来解决。

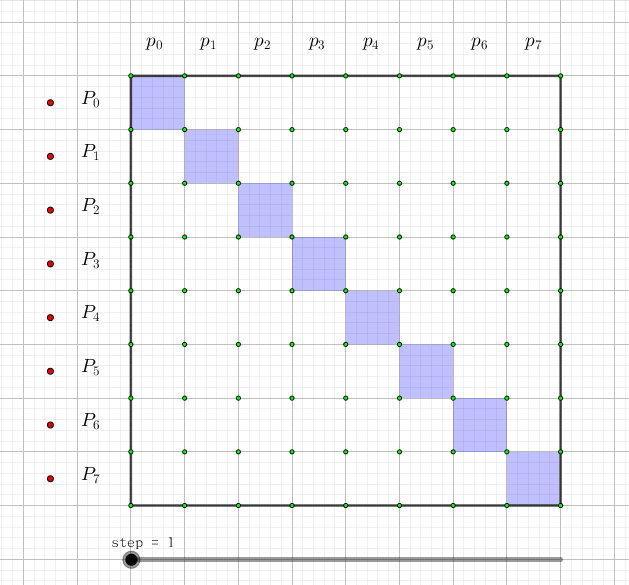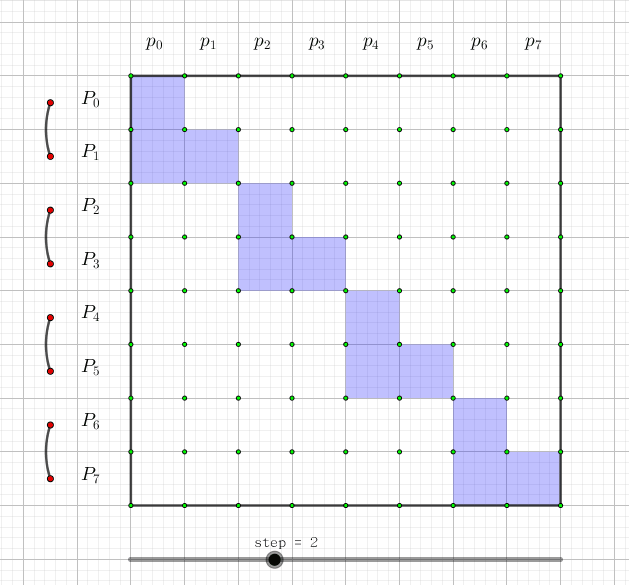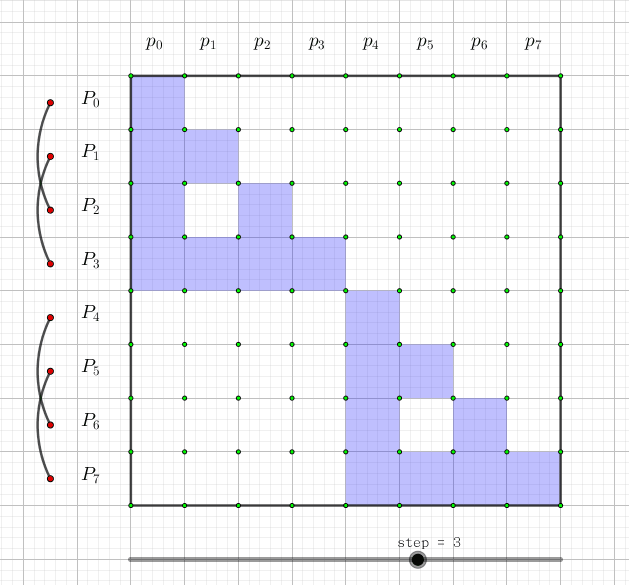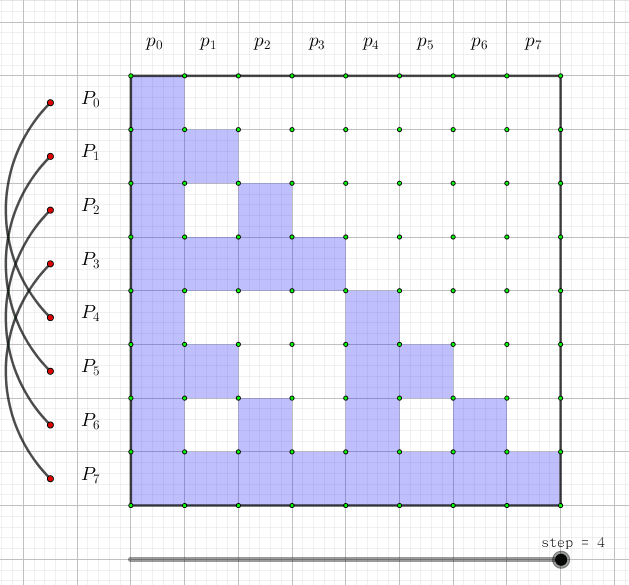
快速莫比乌斯变换是用来解决集合幂级数的集合并卷积的问题，也就是说，给定两个长度为 $2^n-1$ 的序列 $a$ 和 $b$ ，让求一个序列 $c$ 满足： $$ c[k]=\sum_{i\text{ or }j=k}a[i]\times b[j] $$ 暴力做肯定是 $O((2^n)^2)$ 的，考虑怎么优化， $i\cup j=k$ 这个很不好处理，那么我们可以做一个集合的前缀和（用大写字母表示）： $$ \begin{align} C[k]&=\sum_{k_0\subseteq k}c[k_0]\\ &=\sum_{k_0\subseteq k}\sum_{i\cup j=k_0}a[i]\times b[j]\\ &=\sum_{i\cup j\subseteq k}a[i]\times b[j]\\ &=(\sum_{i\subseteq k}a[i])\times (\sum_{j\subseteq k}b[j])\\ &=A[k]\times B[k] \end{align} $$ 也就是说快速莫比乌斯变换就是用来求集合的前缀和的，在这个求完之后像 $FFT$ 一样对应位置相乘然后再变换回去即可。

但是这道题就是让求子集统计，也就是说不用变换回去，维护一个最大值一个次大值即可。

Code：

#include<algorithm>

#include<iostream>

#include<cstdlib>

#include<cstdio>

#include<cmath>

#include<cctype>

#include<cstring>

using namespace std;

int n;

#define MAXN 19

struct state

{

	long long x,y;

	friend state operator + (state a,state b)

	{

		state res;

		if(a.x >= b.x){res.x = a.x;res.y = max(a.y,b.x);}

		else {res.x = b.x;res.y = max(a.x,b.y);}

		return res;

	}

}f[1 << MAXN];

void FMT(state f[],int l)

{

	for(int i = 0;i < l;++i)

	{

		for(int j = 0;j < (1 << l);++j)

		{

			if(((j >> i) & 1) == 0)f[j | (1 << i)] = f[j | (1 << i)] + f[j];

		}

	}

	return;

}

long long ans[1 << MAXN];

int main()

{

	scanf("%d",&n);

	for(int i = 0;i < (1 << n);++i)

	{

		scanf("%lld",&f[i].x);

		f[i].y = -9999999999;

	}

	FMT(f,n);

	for(int i = 0;i < (1 << n);++i)ans[i] = f[i].x + f[i].y;

	for(int i = 1;i < (1 << n);++i)ans[i] = max(ans[i],ans[i - 1]);

	for(int i = 1;i < (1 << n);++i)printf("%lld\n",ans[i]);

	return 0;

}