问题：

给出一些物品和选择物品的限制条件，要求刚好选 $m$ 个，最大化 $/$ 最小化权值和。

我们可以得到一个比较显然的 $DP$ 方程 $f[i][j]$ 表示前 $i$ 个刚好选 $j$ 个的最值，最后的答案就是 $f[n][m]$ ，设 $g[k]=f[n][k]$ ，那么 $g[k]$ 是一个凸函数，也就是说差分之后的数组是单调的。

并且还满足一个条件是如果没有第二维的限制也就是说那么 $DP$ 可以优化到

解决方案：

既然 $g[k]$ 是凸函数，那我们就把他画在坐标系下：

这个时候我们找到的最高点就是 $D$ 点，但是如果我们要求恰好选 $5$ 个的最大值，也就是 $F$ 点，那么就找不到，这个时候我们可以给所有点加上一个偏移量 $C$ ，也就是把点 $(x,y)$ 变成 $(x,y+xC)$ ，比如说 $C=1$ ：

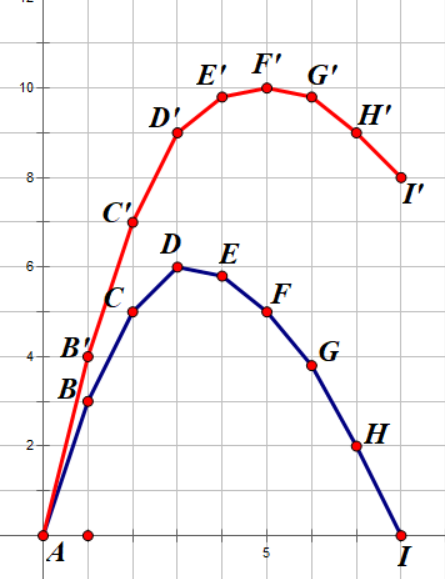
这个时候我们再找就可以找到 $F$ 点，再减掉 $C\times m$ 就是我们想要的答案。

那么这就给了我们一个思路，我们可以给每个物品的代价 $+C$ 然后 $DP$ ，最后再把 $f[n]$ 减掉 $C\times m$ 就行了，复杂度是 $O(n\log n)$ 的。

边界问题：

我们可能会得到一个尴尬的结果：当 $C=x$ 时， $cnt=m-1$ ，当 $C=x+1$ 时， $cnt=m+1$ ，这个时候我们只要保证每次计算的时候只保留最小的那个解，在二分到最后的时候如果极值点不为 $n$ 的话应比 $n$ 小。

#include<algorithm>

#include<iostream>

#include<cstdlib>

#include<cstdio>

#include<cmath>

#include<cstring>

using namespace std;

int n,m,ned;

#define MAXM 100010

struct edge

{

	int u,v,val,col;

}e[MAXM];

bool cmp_val(edge a,edge b){return (a.val == b.val ? a.col < b.col : a.val < b.val);}

#define MAXN 50010

int f[MAXN];

int find(int x){return (f[x] == x ? x : f[x] = find(f[x]));}

int ans;

int query(int k)

{

	ans = 0;

	for(int i = 1;i <= n;++i)f[i] = i;

	for(int i = 1;i <= m;++i)

		if(e[i].col == 0)

			e[i].val += k;

	sort(e + 1,e + 1 + m,cmp_val);

	int res = 0;

	for(int i = 1;i <= m;++i)

	{

		int p = find(e[i].u),q = find(e[i].v);

		if(p == q)continue;

		f[p] = q;

		if(e[i].col == 0)++res;

		ans += e[i].val;

	}

	for(int i = 1;i <= m;++i)

		if(e[i].col == 0)

			e[i].val -= k;

	return res;

}

int main()

{

	scanf("%d%d%d",&n,&m,&ned);

	for(int i = 1;i <= m;++i)

	{

		scanf("%d%d%d%d",&e[i].u,&e[i].v,&e[i].val,&e[i].col);

		++e[i].u;++e[i].v;

	}

	int l = -100,r = 100,mid;

	while(l < r)

	{

		mid = ((l + r + 1) / 2);//cout << mid << endl;

		if(query(mid) >= ned)l = mid;

		else r = mid - 1;

	}//cout << l << endl;

	query(l);

	cout << ans - ned * l << endl;

	return 0;

}