Description：

给你 $n$ 个向量，要求构造两个向量使得从某个点开始用原来向量和整数系数能够线性表示出的坐标恰好也是这两个向量用整数系数能够线性表出的。

$1\leqslant n\leqslant 100$

Solution：

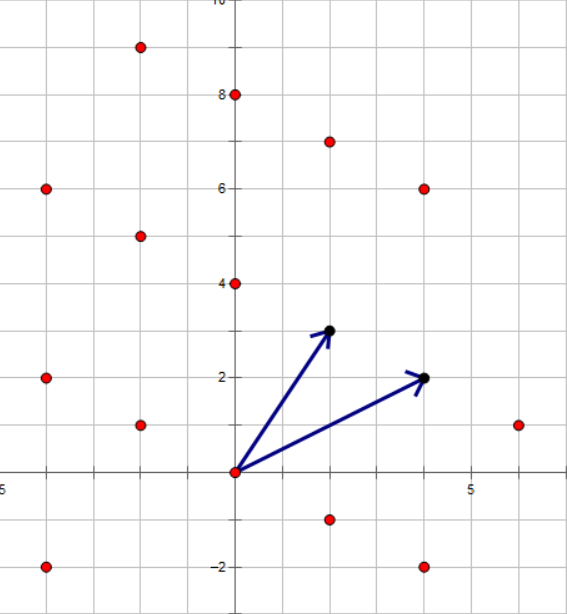
这个图标出了向量 $(2,3)$ 和向量 $(4,2)$ 所能到达的所有点，观察之下可以发现这些点其实可以由向量 $(2,3)$ 和 $(4,0)$ 表出，也就是说我们对于两个向量所能构成的所有点一定可以找到一个向量和另一个在 $y$ 轴上的向量表示出来，又观察一下发现那个不在 $y$ 轴上的向量横坐标一定是 $\gcd(x_1,x_2)$ ，因为由裴蜀定理得只有这样才可以表出所有原来两个横坐标所能表出的横坐标，设那个在 $y$ 轴上的向量为 $(0,l)$ ，那么可以列出方程： $$ \begin{align} ax_1+bx_2&=0\\ ay_1+by_2&=l\\ \end{align} $$ 我们要想得到能够使得 $a$ 和 $b$ 都是整数的最小的 $l$ ，这个方程不能随便解，不然就不能保证 $a,b$ 为整数。

$$ \begin{align} &b=\frac{-ax_1}{x_2}\\ &\because b\in\Z\\ &\therefore x_2|ax_1\\ &\therefore\frac{x_2}{\gcd(x_1,x_2)}|\frac{x_1}{\gcd(x_1,x_2)}a\\ &\because\gcd(\frac{x_1}{\gcd(x_1,x_2)},\frac{x_2}{\gcd(x_1,x_2)})=1\\ &\therefore\frac{x_2}{\gcd(x_1,x_2)}|a \end{align} $$ 设 $a=k\frac{x_2}{\gcd(x_1,x_2)}$ ， $b=-k\frac{x_1}{\gcd(x_1,x_2)}$ ，则 $l=\frac{k(x_2y_1-x_1y_2)}{\gcd(x_1,x_2)}$ ，因为要让 $l$ 最小，所以 $k=1$ ， $l=\frac{|x_2y_1-x_1y_2|}{\gcd(x_1,x_2)}$ 。

然后再考虑那一个不在 $y$ 轴上的向量，他的横坐标必须为 $\gcd(x_1,x_2)$ ，因为由裴蜀定理得 $ax_1+bx_2=k\gcd(x_1,x_2)$ 一定有解，那么我们又可以得到方程： $$ \begin{align} ax_1+bx_2&=\gcd(x_1,x_2)\\ ay_1+by_2&=y \end{align} $$ 由于并不要求 $y$ 最大或最小，因此用扩欧随便解出一组 $a$ 和 $b$ 带到 $y$ 里就行了。

这样我们把每两个向量这么做一下，最后得到了很多 $y$ 轴上的向量，把他们合起来很简单，因为就是他们 $y$ 坐标的 $\gcd$ ，这样我们就找到了这两个向量。

Code：

#include<algorithm>

#include<iostream>

#include<cstdlib>

#include<cstdio>

#include<cmath>

#include<cctype>

#include<cstring>

using namespace std;

typedef long long ll;

ll exgcd(ll a,ll b,ll &x,ll &y)

{

	if(b == 0)

	{

		x = 1;

		y = 0;

		return a;

	}

	ll x_,y_;

	ll g = exgcd(b,a % b,x_,y_);

	x = y_;y = x_ - a / b * y_;

	return g;

}

ll gcd(ll a,ll b){return (b == 0 ? a : gcd(b,a % b));}

#define MAXN 110

int n;

struct vector

{

	ll x,y;

}v[MAXN];

ll l[MAXN];

pair<ll,vector> calc(vector a,vector b)

{

	pair<ll,vector> res;

	res.first = llabs(b.x * a.y - a.x * b.y) / gcd(a.x,b.x);

	res.second.x = gcd(a.x,b.x);

	ll a_,b_;

	exgcd(a.x,b.x,a_,b_);

	res.second.y = a_ * a.y + b_ * b.y;

	return res;

}

int main()

{

	scanf("%d",&n);

	for(int i = 1;i <= n;++i)

	{

		scanf("%lld%lld",&v[i].x,&v[i].y);

	}

	for(int i = 2;i <= n;++i)

	{

		pair<ll,vector> res = calc(v[i - 1],v[i]);

		l[i - 1] = res.first;

		v[i] = res.second;

	}

	ll g = l[1];

	for(int i = 2;i < n;++i)

	{

		g = gcd(g,l[i]);

	}

	cout << 0 << " " << g << endl << v[n].x << " " << v[n].y << endl;

	return 0;

}