Description：

$n$ 个 $1$ 和 $m$ 个 $0$ 组成字符串，要求组成的字符串任意的前k个字符中， $1$ 的个数不能少于 $0$ 的个数。求满足要求的字符串共有多少个。

$1\le n \le 1000000$

Solution：

当 $n=m$ 时就是卡特兰数，当 $n\ne m$ 时，也可以考虑利用卡特兰数折线原理来求。

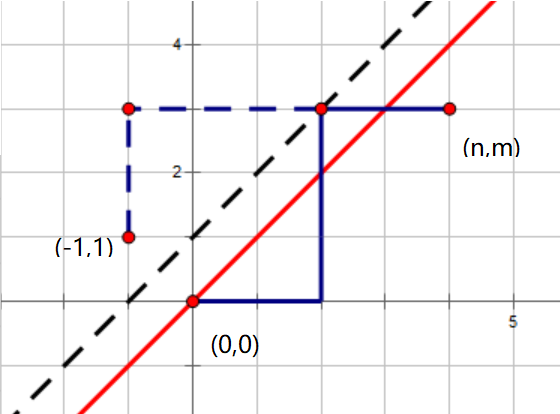
如果把向右走看作 $1$ ，向上走看作 $0$ ，那么一个字符串就是从 $(0,0)$ 走到 $(n,m)$ 只向右和向上走的方案数，为 $C_{m}^{n+m}$ ，意义是在共 $n+m$ 步中选出 $m$ 步向上走，考虑减掉不合法的情形，放在图上看也就是跨过直线 $y=x$ 的路径，既然跨过了，那它一定会到达直线 $y=x+1$ ，把他第一个到这条直线的点之前的部分按 $y=x+1$ 对称，可以发现每一个不合法的路径都对应一个从 $(-1,1)$ 开始的路径，所以本题答案为 $C_m^{n+m}-C^{n+m}_{m-1}$ 。

模数是质数，组合数可以预处理阶乘和逆元算。

Code：

#include<algorithm>

#include<iostream>

#include<cstdlib>

#include<cstdio>

#include<cmath>

#include<cstring>

using namespace std;

typedef long long ll;

ll n,m;

#define MOD 20100403

#define MAXN 2000010

ll power(ll a,ll b)

{

	ll res = 1;

	while(b > 0)

	{

		if(b & 1)res = res * a % MOD;

		a = a * a % MOD;

		b = b >> 1;

	}

	return res;

}

ll fac[MAXN],inv[MAXN];

ll C(ll n,ll m)

{

	return fac[n] * inv[m] % MOD * inv[n - m] % MOD;

}

int main()

{

	cin >> n >> m;

	fac[0] = 1;

	for(ll i = 1;i <= n + m;++i)fac[i] = fac[i - 1] * i % MOD;

	inv[n + m] = power(fac[n + m],MOD - 2);

	for(ll i = n + m - 1;i >= 0;--i)inv[i] = inv[i + 1] * (i + 1) % MOD;

	cout << (C(n + m,n) - C(n + m,m - 1) + MOD) % MOD << endl;

	return 0;

}