Description：

给出平面上任意三点不共线任意四点不共圆的一些点，每次随机选三个点画圆，问期望包括进几个点。

$1\leqslant n\leqslant 1500$

Solution：

考虑计算每个点对答案的贡献，分情况讨论：

第一种情况： $A,B,C,D$ 形成了一个凹四边形，除了圆上的点这个凹四边形会多产生一个贡献：

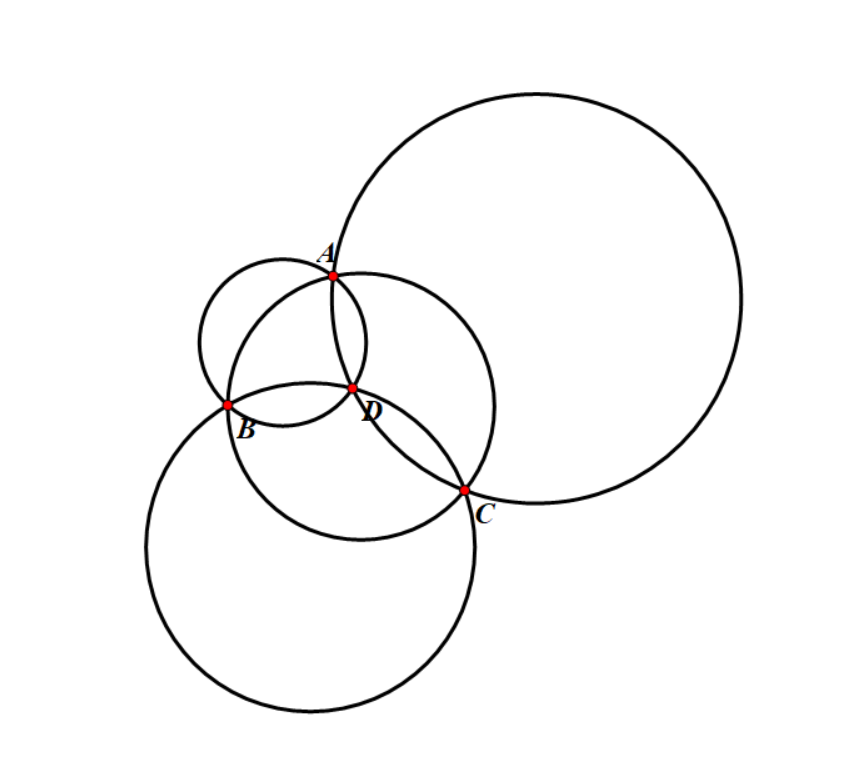
第二种情况： $A,B,C,D$ 构成了一个凸四边形，除了圆上的点会对答案产生 $2$ 的贡献：

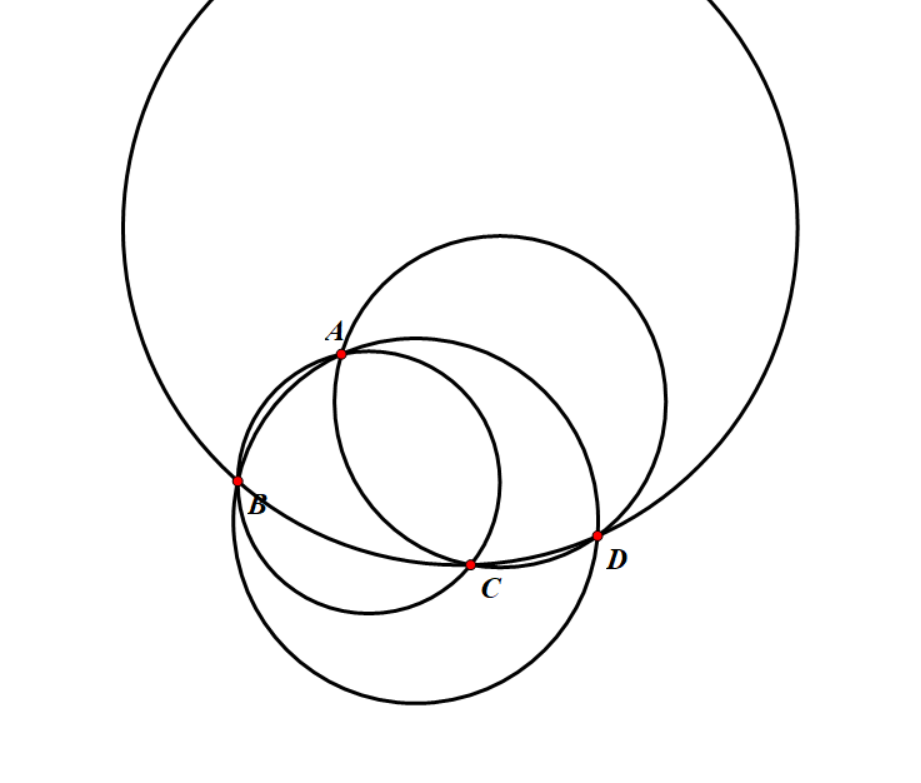
由于四边形总数是 $\binom n4$ ，因此我们只要计算出凹四边形或者凸四边形中的一个即可求出对答案的总贡献，即： $$ ans=3+\frac{凹四边形+凸四边形\times 2}{\binom n3} $$ 考虑计算凹四边形的个数，枚举每个点作为凹点，这样可以保证补充不漏，然后凹四边形就等于 $\binom {n-1}3-$ 凸四边形，那么我们就枚举另一个点，同时用双指针维护和他之间度数尽量大但是又不大于 $180^\circ$ 的另一个点，从这个区域内任选两个点就是答案。

Code：

#include<algorithm>

#include<iostream>

#include<cstdlib>

#include<cstdio>

#include<cmath>

#include<cctype>

#include<cstring>

using namespace std;

inline int rd()

{

	register int res = 0,f = 1;register char c = getchar();

	while(!isdigit(c)){if(c == '-')f = -1;c = getchar();}

	while(isdigit(c))res = (res << 1) + (res << 3) + c - '0',c = getchar();

	return res * f;

}

int n;

#define MAXN 3010

typedef long long ll;

struct point

{

	ll x,y;

	double ang;

}p[MAXN],p_[MAXN];

point operator - (point a,point b){return (point){a.x - b.x,a.y - b.y};}

ll operator * (point a,point b){return a.x * b.y - a.y * b.x;}

double angle(point k){return atan2(k.y,k.x);}

int tot = 0;

ll C[MAXN][5];

bool cmp_ang(point a,point b){return a.ang < b.ang;}

ll calc(int k)

{

	tot = 0;

	for(int i = 1;i <= n;++i)if(i != k)p_[++tot] = p[i];

	for(int i = 1;i <= tot;++i)p_[i].ang = angle(p_[i] - p[k]);

	sort(p_ + 1,p_ + 1 + tot,cmp_ang);

	for(int i = tot + 1;i <= 2 * tot;++i)p_[i] = p_[i - tot];

	ll sum = 0;

	for(int i = 1,j = 1;i <= tot;++i)

	{

		j = max(i,j);

		while((p_[j + 1] - p[k]) * (p_[i] - p[k]) < 0)++j;

		sum += C[j - i][2];

	}

	return C[n - 1][3] - sum;

}

int main()

{

	scanf("%d",&n);

	for(int i = 1;i <= n;++i)p[i].x = rd(),p[i].y = rd();

	for(int i = 0;i <= n;++i)C[i][0] = 1;

	for(int i = 1;i <= n;++i)for(int j = 1;j <= 4;++j)C[i][j] = C[i - 1][j] + C[i - 1][j - 1];

	ll sum = 0;

	for(int k = 1;k <= n;++k)sum += calc(k);

	printf("%.10lf\n",3 + 1.0 * (C[n][4] * 2 - sum) / C[n][3]);

	return 0;

}