Description：

给一个 $n\times n$ 的矩阵 $B$ 和一个 $1\times n$ 的矩阵 $C$ 。求一个 $1\times n$ 的 $01$ 矩阵 $A$ 。使得 $D=(A\times B-C)\times A^{\sf T}$ ，求 $D$ 。

$1\leqslant n\leqslant 500$

Solution：

把式子拆开： $$ D=\sum_{i=1}^n\sum_{j=1}^n A[i]A[j]B[i][j]-\sum_{i=1}^nA[i]C[i] $$ 我们可以把这个式子理解成：

如果选 $i$ ，会有 $C[i]$ 的代价，如果 $i$ 和 $j$ 都选，会有 $B[i][j]+B[j][i]$ 的收益，最大化答案。

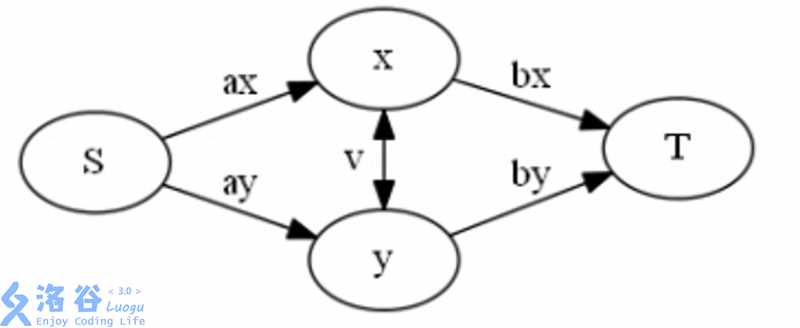
还是利用这个图，如果和最小割中这个点和 $S$ 在一起代表选他，我们可以列出一些方程： $$ \begin{align} &b_x+b_y=C[x]+C[y]\\ &a_x+a_y=B[x][x]+B[y][y]+B[x][y]+B[y][x]\\ &a_y+v+b_x=B[y][y]+B[x][y]+B[y][x]+C[x]\\ &a_x+v+b_y=B[x][x]+B[x][y]+B[y][x]+C[y]\\ \end{align} $$ 解得： $$ \begin{align} &b_x=C[x]\\ &b_y=C[y]\\ &a_x=B[x][x]+\frac{B[x][y]+B[y][x]}2\\ &a_y=B[y][y]+\frac{B[x][y]+B[y][x]}2\\ &v=\frac{B[x][y]+B[y][x]}2\\ \end{align} $$ 因为代价累加，所以： $$ a_x=B[x][x]+\frac{\sum_{y=1}^n(y\ne x)B[x][y]+B[y][x]}2=\frac{\sum_{y=1}^nB[x][y]+B[y][x]}2 $$ 然后跑最小割就行了。

Code：

#include<algorithm>

#include<iostream>

#include<cstdlib>

#include<cstdio>

#include<cmath>

#include<queue>

#include<cctype>

#include<cstring>

using namespace std;

int n;

#define MAXN 510

int B[MAXN][MAXN];

int C[MAXN];

struct edge

{

	int to,nxt,f;

}e[(MAXN * MAXN + MAXN * 2) * 2];

int edgenum = 0;

int lin[MAXN * MAXN];

void add(int a,int b,int f)

{

	e[edgenum] = (edge){b,lin[a],f};lin[a] = edgenum++;

	e[edgenum] = (edge){a,lin[b],0};lin[b] = edgenum++;

	return;

}

int id(int i,int j){return (i - 1) * n + j;}

int s,t;

int ch[MAXN * MAXN];

bool BFS()

{

	memset(ch,-1,sizeof(ch));

	ch[s] = 0;

	queue<int> q;q.push(s);

	while(!q.empty())

	{

		int k = q.front();q.pop();

		for(int i = lin[k];i != -1;i = e[i].nxt)

		{

			if(ch[e[i].to] == -1 && e[i].f)

			{

				ch[e[i].to] = ch[k] + 1;

				q.push(e[i].to);

			}

		}

	}

	return (ch[t] != -1);

}

int flow(int k,int f)

{

	if(k == t)return f;

	int r = 0;

	for(int i = lin[k];i != -1 && f > r;i = e[i].nxt)

	{

		if(ch[e[i].to] == ch[k] + 1 && e[i].f)

		{

			int l = flow(e[i].to,min(f - r,e[i].f));

			e[i].f -= l;r += l;e[i ^ 1].f += l;

		}

	}

	if(r == 0)ch[k] = -1;

	return r;

}

int dinic()

{

	int ans = 0,r;

	while(BFS())while(r = flow(s,0x3f3f3f3f))ans += r;

	return ans;

}

int main()

{

	memset(lin,-1,sizeof(lin));

	scanf("%d",&n);

	int ans = 0;

	for(int i = 1;i <= n;++i)for(int j = 1;j <= n;++j)scanf("%d",&B[i][j]);

	for(int i = 1;i <= n;++i)for(int j = 1;j <= n;++j)ans += B[i][j];

	for(int i = 1;i <= n;++i)scanf("%d",&C[i]);

	s = n * n + 1;t = s + 1;

	for(int i = 1;i <= n;++i)

	{

		int sum = 0;

		for(int j = 1;j <= n;++j)sum += B[i][j] + B[j][i];

		add(s,i,sum);add(i,t,2 * C[i]);

	}

	for(int i = 1;i <= n;++i)for(int j = 1;j <= n;++j)add(i,j,B[i][j] + B[j][i]);

	cout << ans - dinic() / 2 << endl;

	return 0;

}