Description：

给一棵广义线段树，设 $S_{[l,r]}$ 表示定位区间 $[l,r]$ 定位到的点的集合，多次询问 $u,l,r$ 表示求： $$ \sum_{v\in S_{[l,r]}}dis(u,v) $$ $1\leqslant n\leqslant 2\times 10^5$

Solution：

先解决第一个问题，给一棵广义线段树和一个询问区间 $[l,r]$ ，如何求出 $S_{[l,r]}$ ，首先找到在线段树上最短的完全包含询问区间的原区间，也就是第一个开始向左向右同时递归的区间，这个就是 $[l,l]$ 和 $[r,r]$ 在线段树上的 $LCA$ ，从这个点往左右两边看，会发现是一个前缀和一个后缀，我们需要把这些区间找出来。

为了做到这一点，我们可以定义一个”广义树状数组“，具体来说就是设每个点的 $father$ 为它向后找找到的第一个紧挨着他的区间，或者说是每个点只存储半边的信息，画个图说比较清楚：

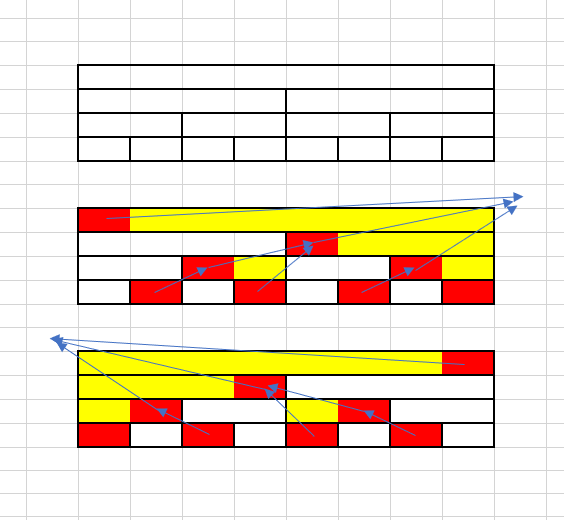
这三个图分别是原树、查询后缀时候的树和查询前缀时候的树，不难发现这个和树状数组非常像，事实上树状数组的本质就是只保留左儿子的zkw线段树，但是在这棵树上由于划分不平均，因此不能用 $lowbit$ 找父亲，我们必须手动把这棵“广义树状数组”建出来，具体构建方法是设 $fa[i]$ 表示 $i$ 这个点在广义树状数组上的 $fa$ ，加入我们现在构建的是前缀树，也就是最后一个图的情况，我们可以先 $fa[lc]=fa[k]$ ，然后 $dfs$ 左儿子，然后 $fa[rc]=lc$ ， $dfs$ 右儿子，然后删掉所有右儿子的点，就得到了一棵广义树状数组。

有了这个，我们就可以求出在线段树上给出一个区间会被分到哪些区间上，就是从每个位置开始往上跳一直跳到跳出去为止，考虑化简答案： $$ \begin{align} ans&=\sum_{v\in S_{[l,r]}}dis(u,v)\\ &=\sum_{v\in S_{[l,r]}}dep[u]+dep[v]-2\times dep[LCA(u,v)]\\ &=|S_{[l,r]}|\times dep[u]+\sum_{v\in S_{[l,r]}}dep[v]-2\times\sum_{v\in S_{[l,r]}}dep[LCA(u,v)] \end{align} $$ 前两项都很好求，麻烦的是最后一项，好像直接搞很不好做，因为 $S_{[l,r]}$ 不一定是一个区间，但是一定是连续的深度递增的一条链，于是可以差分成 $(1,p)-(1,fa[q])$ ，然后从 $1$ 开始 $dfs$ 每次插入删除元素就好了。

Code：