Description：

$n$ 个位置，每个位置有两种状态 $0/1$ ，每次操作这个位置的状态变成他两旁状态的异或值，两端的变成那个与它相邻的状态，求 $T$ 次操作之后整个序列的状态。

$2\leqslant n\leqslant 10^5,1\leqslant T\leqslant10^{18}$

Solution：

如果做过 洛谷3937 changing 那道题的话，这道题就不难想到应该与组合数的奇偶性有关，画个图发现是偶数行的组合数为奇数的位置会影响这个位置的状态。

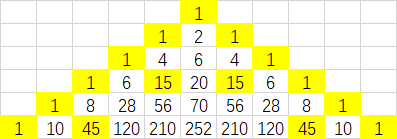
也就是说如果一共进行了 $T$ 次操作，那么位置 $i$ 会对位置 $j$ 产生影响当 ${2T\choose T+i-j}$ 为奇数，先假设这个是一个环，那么就有一个 $n^2$ 做法判断每两个位置是否会产生影响，但是显然跑不过，组合数有一个重要的性质是 $2^i\choose k$ 仅在 $k=2^i$ 或 $k=0$ 时是奇数，那么就可以类似快速幂的做法，把 $T$ 二进制分解，每次就可以 $O(n)$ 求每一位的答案了。

但是这是在序列上，于是有一个很神奇的转化就是把序列复制一份，头和头，尾和尾用一个 $0$ 接起来，这样每个位置都是由左右两边确定，而那么用来你拼接的 $0$ 永远都是 $0$ ，因为他两侧永远都相同，而且成了一个环。

时间复杂度 $O(n\log T)$

Code：

#include<algorithm>

#include<iostream>

#include<cstdlib>

#include<cstdio>

#include<cmath>

#include<cstring>

using namespace std;

int n;

long long t;

#define MAXN 1000010

int a[MAXN];

int b[MAXN];

inline int getc()

{

	register char c = getchar();

	while(c != '0' && c != '1')c = getchar();

	return c - '0';

}

int main()

{

	freopen("C.in","r",stdin);

	freopen("C.out","w",stdout);

	scanf("%d%lld",&n,&t);

	for(int i = 1;i <= n;++i)a[i] = getc();

	a[++n] = 0;

	for(int i = n + 1;i <= 2 * n;++i)

	{

		a[i] = a[2 * n - i];

	}

	n *= 2;

	long long x = 1;

	while(t > 0)

	{

		if(t & 1)

		{

			for(int i = 1;i <= n;++i)

			{

				b[i] = a[((i - x) % n - 1 + n) % n + 1] ^ a[((i + x) % n - 1 + n) % n + 1];

			}

			for(int i = 1;i <= n;++i)a[i] = b[i];

		}

		x = x * 2;

		t = t >> 1;

	}

	for(int i = 1;i <= n / 2 - 1;++i)

	{

		printf("%d",a[i]);

	}

	puts("");

	fclose(stdin);

	fclose(stdout);

	return 0;

}