GDOI模拟 hole

wjh15101051's space

卧薪尝胆，厚积薄发。

GDOI模拟 hole

Date: Thu Sep 06 14:29:26 CST 2018

In Category: NoCategory

Description：

在一个平面直角坐标系中，有 $n$ 个操作， $1$ ，标记点 $(x,y)$ ， $2$ ，询问 $(x,y)$ , $(x+d,y)$ , $(x,y + d)$ 这个等腰直角三角形中有多少被标记的点。

$1\le n \le 88888$

Solution:

发现题目要求的就是：

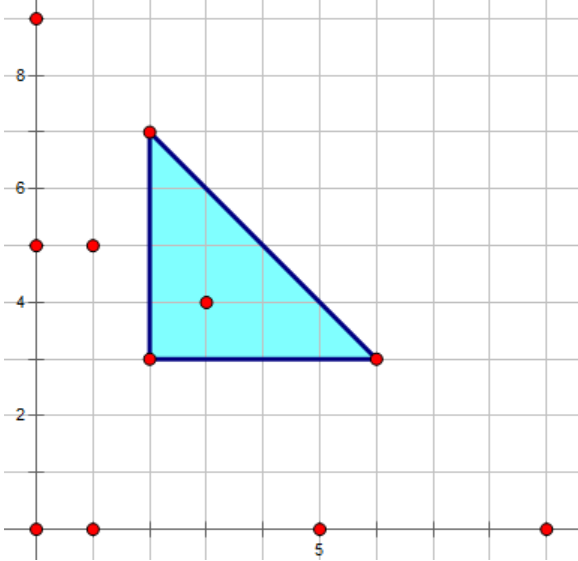
但是这个非常不好求，考虑换一种方式使得可以用一种更方便的方法求，考虑如何把右上角的斜边变为平行于坐标系，可以把 $(x,y)$ 变成 $(x,x+y)$ ，就会变成：

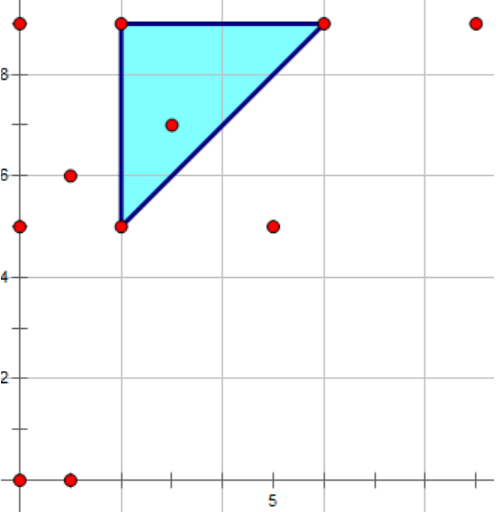
这样上方原本斜的边就变平了，可以直接统计。通过使用二位前缀和，如下：

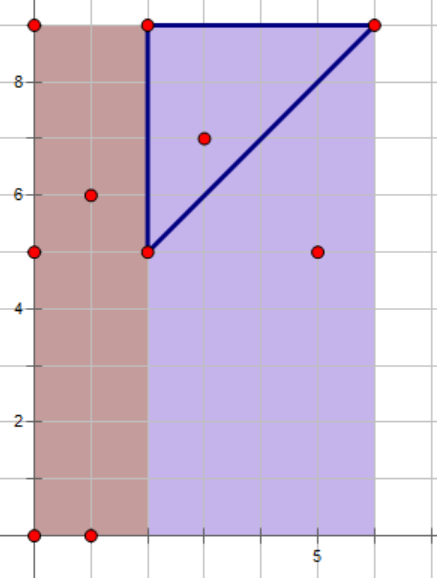
通过使用 $CDQ$ 分治在二维平面上前缀数点，用大的减小的即可得到右边灰色部分的点数，在原图中就是这样：

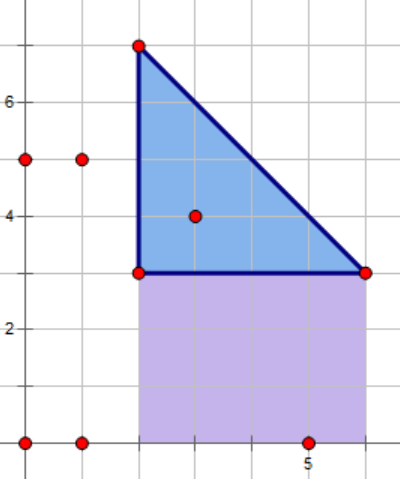
这样下面的也是一个矩形，再做一遍 $CDQ$ 分治二维前缀数点即可计算出下面那部分的点数。

Code：

$RE70$ 调不出来了。


#include<algorithm>

#include<iostream>

#include<cstdlib>

#include<cstdio>

#include<cmath>

#include<cstring>

using namespace std;

int n;

#define MAXN 100000

struct opt

{

	int x,y,d;

}o[MAXN];

struct scan

{

	int pos,x,y,id,type;

}s[MAXN << 2];

bool cmp_x(scan a,scan b){return a.x < b.x;}

bool cmp_pos(scan a,scan b){return a.pos < b.pos;}

int cnt = 0;

int ans[MAXN];

#define MAXX 8000000

int c[MAXX];

int lowbit(int x){return (x & (-x));}

void add(int p,int k)

{

	for(int i = p;i < MAXX;i += lowbit(i))c[i] += k;

	return;

}

int query(int p)

{

	int res = 0;

	for(int i = p;i >= 1;i -= lowbit(i))res += c[i];

	return res;

}

void cdq(int l,int r)

{

	if(l == r)return;

	int mid = ((l + r) >> 1);

	cdq(l,mid);cdq(mid + 1,r);

	sort(s + l,s + mid + 1,cmp_x);sort(s + mid + 1,s + r + 1,cmp_x);

	int i = l,j = mid + 1;

	for(;i <= mid && j <= r;)

	{

		if(s[i].x <= s[j].x)

		{

			if(s[i].type == 0)

			{

				add(s[i].y,1);

			}

			++i;

		}

		else

		{

			if(s[j].type != 0)

			{

				ans[s[j].id] += query(s[j].y) * s[j].type;

			}

			++j;

		}

	}

	for(;j <= r;++j)

		if(s[j].type != 0)

			ans[s[j].id] += query(s[j].y) * s[j].type;

	for(int k = l;k < i;++k)

		if(s[k].type == 0)

			add(s[k].y,-1);

	sort(s + l,s + r + 1,cmp_pos);

	return;

}

int main()

{

	memset(c,0,sizeof(c));

	scanf("%d",&n);

	for(int i = 1;i <= n;++i)

	{

		scanf("%d%d%d",&o[i].x,&o[i].y,&o[i].d);

		o[i].x += 3;o[i].y += 3;

	}

	memset(ans,0,sizeof(ans));

	cnt = 0;

	for(int i = 1;i <= n;++i)

	{

		if(o[i].d == 0)

		{

			++cnt;s[cnt] = (scan){cnt,o[i].x,o[i].y,0,0};

		}

		else

		{

			++cnt;s[cnt] = (scan){cnt,o[i].x - 1,o[i].y - 1,i,1};

			++cnt;s[cnt] = (scan){cnt,o[i].x + o[i].d,o[i].y - 1,i,-1};

		}

	}

	cdq(1,cnt);

	cnt = 0;

	for(int i = 1;i <= n;++i)

	{

		if(o[i].d == 0)

		{

			++cnt;s[cnt] = (scan){cnt,o[i].x,o[i].x + o[i].y,0,0};

		}

		else

		{

			++cnt;s[cnt] = (scan){cnt,o[i].x - 1,o[i].x + o[i].y + o[i].d,i,-1};

			++cnt;s[cnt] = (scan){cnt,o[i].x + o[i].d,o[i].x + o[i].d + o[i].y,i,1};

		}

	}

	cdq(1,cnt);

	for(int i = 1;i <= n;++i)

		if(o[i].d != 0)

			printf("%d\n",ans[i]);

	return 0;

}

In tag: 数据结构-CDQ分治

wjh15101051