Description：

一个 $N\times M$ 的网格，每个网格都有 $p_{i,j}$ 的概率被堵塞，如果一个格子在边界或者周围有没有被堵塞的格子，那他下一秒就会被清理，问每个点被清理所用的平均时间。

$1\leqslant n \leqslant 200$

Solution：

设 $s[k][i][j]$ 表示格子 $(i,j)$ ，用至少 $k$ 的时间才能清空的概率，要想至少 $k$ 的时间，所有和他曼哈顿距离在 $k-1$ 以内的点都必须没有被清空，也就是这些点概率的乘积，其他的点可以随意，关于这个如何在 $O(n^3)$ 的时间内求，可以用前缀和，如下：

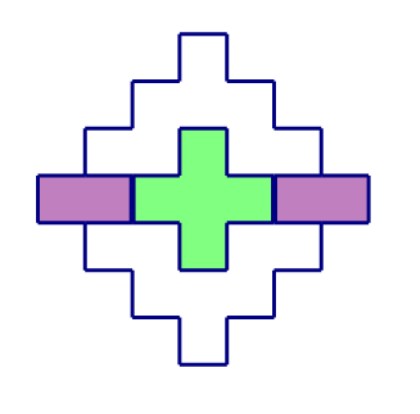
整个的值就是上面距离小一的值加下面距离小一的值减去中间绿色重复的值加上左右两边紫色的部分，那么 $(i.j)$ 的答案就是 $\begin{align}\sum_{k=1}^{\min(n,m)}(s[k][i][j]-s[k+1][i][j])\times k\end{align}$ 。

Code：

#include<algorithm>

#include<iostream>

#include<cstdlib>

#include<cstdio>

#include<cmath>

#include<cstring>

using namespace std;

int n,m;

#define MAXN 210

int s[MAXN][MAXN][MAXN];

int p[MAXN * 3][MAXN * 3];

#define MOD 1000000007

typedef long long ll;

int power(int a,int b)

{

	int res = 1;

	while(b > 0)

	{

		if(b & 1)res = 1ll * res * a % MOD;

		a = 1ll * a * a % MOD;

		b = b >> 1;

	}

	return res;

}

int inv(int k)

{

	return power(k,MOD - 2);

}

int main()

{

	scanf("%d%d",&n,&m);

	int a,b;

	memset(p,0,sizeof(0));

	for(int i = 1;i <= n;++i)

	{

		for(int j = 1;j <= m;++j)

		{

			scanf("%d%d",&a,&b);

			p[i + MAXN][j + MAXN] = 1ll * a * inv(b) % MOD;

		}

	}

	for(int i = 1;i <= n;++i)

	{

		for(int j = 1;j <= m;++j)

		{

			s[1][i][j] = p[i + MAXN][j + MAXN];

		}

	}

	for(int i = 1;i <= n;++i)

	{

		for(int j = 1;j <= m;++j)

		{

			s[2][i][j] = 1ll * p[i + MAXN][j + MAXN] * p[i + MAXN - 1][j + MAXN] % MOD * p[i + MAXN + 1][j + MAXN] % MOD * p[i + MAXN][j + MAXN + 1] % MOD * p[i + MAXN][j + MAXN - 1] % MOD;

		}

	}

	for(int k = 3;k <= max(n,m);++k)

	{

		for(int i = 1;i <= n;++i)

		{

			for(int j = 1;j <= m;++j)

			{

				int a = 1ll * s[k - 1][i - 1][j] * s[k - 1][i + 1][j] % MOD * inv(s[k - 2][i][j]) % MOD;

				int b = 1ll * p[i + MAXN][j - k + 1 + MAXN] * p[i + MAXN][j - k + 2 + MAXN] % MOD * p[i + MAXN][j + k - 1 + MAXN] % MOD * p[i + MAXN][j + k - 2 + MAXN] % MOD;

				s[k][i][j] = 1ll * a * b % MOD;

			}

		}

	}

	for(int i = 1;i <= n;++i)

	{

		for(int j = 1;j <= m;++j)

		{

			int ans = 0;

			for(int k = 1;k < max(n,m);++k)

			{

				ans = (ans + 1ll * (s[k][i][j] - s[k + 1][i][j] + MOD) % MOD * k % MOD) % MOD;

			}

			cout << ans << " ";

		}

		cout << endl;

	}

	return 0;

}