Description：

有一个链的集合，链有权值，支持插入一条链或者删除一条链，在树上找一条链使得和他相交的链权值和最大。

$1\leqslant n\leqslant 10^5$

Solution：

首先两条链相交的充分必要条件是：一条链的 $LCA$ 在另一条链上。

然后考虑动态 $DP$ ，或者从链分治的角度更好理解，我们在全局维护一个堆，每条重链在堆中有一个元素，代表最终选出的链的 $LCA$ 在这条重链上的最大值。

然后再分两种情况，一是最后选出的点只有一个点在 $LCA$ 所在的重链上，也就是说来自两个轻子树，那么我们可以在每个点维护轻儿子的可删堆中查询最大值和次大值即可。具体做法是每个点记录一下轻儿子里的次大值，然后在线段树的叶子统计这样的答案，如果是最小值，就直接加，否则和原来的次大值做差累加到答案里，第二种情况是一条链和重链的交也是连续的一段，因此我们可以用类似链上最大子段和来计算，可以用线段树维护，我们把所有的贡献分成两部分，一是这条选出链的 $LCA$ 在令一条链的非 $LCA$ 节点上，二是另一条链的 $LCA$ 在这条链上，对于第一种，我们先把另一条链的 $LCA$ 挖掉，然后做区间加，但是这个区间加只会加包括最高点的答案的权，也就是 $rs$ 和 $ms$ ，见下图：

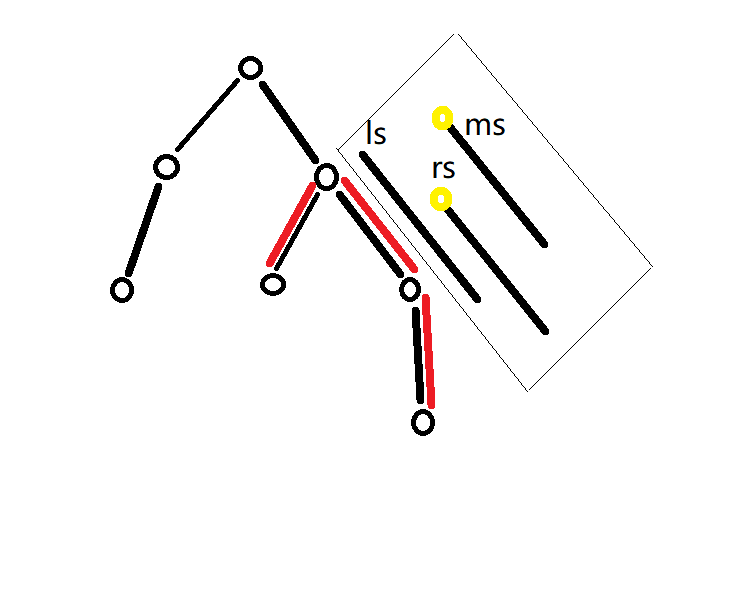然后第二种就是单点加，也可以用线段树做，一定注意各种细节。

Code：

#include<algorithm>

#include<iostream>

#include<cstdlib>

#include<cstdio>

#include<cmath>

#include<queue>

#include<cctype>

#include<cstring>

using namespace std;

typedef long long ll;

int n,m;

#define MAXN 100010

inline int rd(){

	register int res = 0,f = 1;register char c = getchar();

	while(!isdigit(c)){if(c == '-')f = -1;c = getchar();}

	while(isdigit(c))res = (res << 1) + (res << 3) + c - '0',c = getchar();

	return res * f;

}

inline char getc(){

	register char c = getchar();while(c != '+' && c != '-')c = getchar();return c;

}

struct query{int u,v,w;}q[MAXN];

struct edge{int to,nxt;}e[MAXN << 1];

int edgenum = 0,lin[MAXN] = {0};

void add(int a,int b){

	e[++edgenum] = (edge){b,lin[a]};lin[a] = edgenum;

	e[++edgenum] = (edge){a,lin[b]};lin[b] = edgenum;

}

struct heap{

	priority_queue<ll> add,del;

	void insert(ll k){add.push(k);}

	void remove(ll k){del.push(k);}

	ll top(){

		while(!del.empty() && add.top() == del.top())add.pop(),del.pop();

		if(!add.empty())return add.top();else return 0;

	}

	void pop(){

		while(!del.empty() && add.top() == del.top())add.pop(),del.pop();

		if(!add.empty())add.pop();return;

	}

	ll se(){

		ll k = top();pop();ll v = top();insert(k);return v;

	}

}ans,g[MAXN];

int dep[MAXN],siz[MAXN],son[MAXN],top[MAXN],bot[MAXN],fa[MAXN];

int rnk[MAXN],th[MAXN],tot = 0;

void dfs1(int k,int depth){

	siz[k] = 1;dep[k] = depth + 1;

	for(int i = lin[k];i != 0;i = e[i].nxt){

		if(e[i].to == fa[k])continue;

		fa[e[i].to] = k;dfs1(e[i].to,depth + 1);siz[k] += siz[e[i].to];

		if(son[k] == 0 || siz[e[i].to] > siz[son[k]])son[k] = e[i].to;

	}

}

void dfs2(int k,int tp){

	top[k] = tp;rnk[k] = ++tot;th[tot] = k;

	if(son[k] == 0){bot[k] = k;return;}dfs2(son[k],tp);bot[k] = bot[son[k]];

	for(int i = lin[k];i != 0;i = e[i].nxt){

		if(e[i].to == fa[k] || e[i].to == son[k])continue;

		dfs2(e[i].to,e[i].to);g[k].insert(0);

	}

}

struct node{

	int lc,rc;ll ls,rs,ss,ms,tag;

	node(){lc = rc = ls = rs = ss = ms = tag = 0;}

}t[MAXN << 1];

int root,ptr = 0;

int newnode(){return ++ptr;}

#define mid ((l + r) >> 1)

void build(int &rt,int l,int r){

	rt = newnode();if(l == r)return;

	build(t[rt].lc,l,mid);build(t[rt].rc,mid + 1,r);

}

node merge(node rt,node lc,node rc){

	rt.ss = lc.ss + rc.ss;rt.ms = max(max(lc.ms,rc.ms),lc.rs + rc.ls);

	rt.ls = max(lc.ls,lc.ss + rc.ls);rt.rs = max(rc.rs,rc.ss + lc.rs);return rt;

}

void pushdown(int rt){

	t[t[rt].lc].rs += t[rt].tag;t[t[rt].lc].ms += t[rt].tag;t[t[rt].lc].tag += t[rt].tag;

	t[t[rt].rc].rs += t[rt].tag;t[t[rt].rc].ms += t[rt].tag;t[t[rt].rc].tag += t[rt].tag;

	t[rt].tag = 0;

}

void add(int rt,int L,int R,ll k,int l,int r){

	if(L <= l && r <= R){t[rt].rs += k;t[rt].ms += k;t[rt].tag += k;return;}

	pushdown(rt);

	if(L <= mid)add(t[rt].lc,L,R,k,l,mid);if(R > mid)add(t[rt].rc,L,R,k,mid + 1,r); 

	t[rt] = merge(t[rt],t[t[rt].lc],t[t[rt].rc]);

}

node query(int rt,int L,int R,int l,int r){

	if(L <= l && r <= R)return t[rt];

	pushdown(rt);

	if(R <= mid)return query(t[rt].lc,L,R,l,mid);

	if(L > mid)return query(t[rt].rc,L,R,mid + 1,r);

	return merge(t[rt],query(t[rt].lc,L,R,l,mid),query(t[rt].rc,L,R,mid + 1,r));

}

ll ci[MAXN],cur;

void change(int rt,int p,ll k,int tag,int l,int r){//tag=2 ¸üдγ¤Á´ tag=1 ¸üе¥Á´Çá×ÓÊ÷ tag=0 LCA´¦µ¥µã¼Ó

	if(l == r){

		if(tag == 2){ll d = k - ci[cur];ci[cur] = k;t[rt].ms += d;return;}

		t[rt].ls += k;t[rt].rs += k;t[rt].ms += k;if(tag == 0)t[rt].ss += k;

		return;

	}

	pushdown(rt);

	if(p <= mid)change(t[rt].lc,p,k,tag,l,mid);else change(t[rt].rc,p,k,tag,mid + 1,r);

	t[rt] = merge(t[rt],t[t[rt].lc],t[t[rt].rc]);

	return;

}

void add(int a,int b,int w){

	while(top[a] != top[b]){

		if(dep[top[a]] < dep[top[b]])swap(a,b);

		add(root,rnk[top[a]],rnk[a],w,1,n);

		a = fa[top[a]];

	}

	if(dep[a] > dep[b])swap(a,b);

	add(root,rnk[a] + 1,rnk[b],w,1,n);

	int lca = a;

	change(root,rnk[lca],w,0,1,n);

	return;

}

ll val[MAXN],len[MAXN];

void calc(int k){

	while(k){

		k = top[k];node v = query(root,rnk[k],rnk[bot[k]],1,n);

		ans.remove(val[k]);val[k] = v.ms;ans.insert(val[k]);

		int f = fa[k];if(f == 0)break;

		ll la = g[f].top();g[f].remove(len[k]);len[k] = v.ls;g[f].insert(len[k]);

		change(root,rnk[f],g[f].top() - la,1,1,n);

		cur = f;change(root,rnk[f],g[f].se(),2,1,n);

		k = f;

	}

	return;

}

int main(){

	scanf("%d%d",&n,&m);

	for(int i = 1;i < n;++i)add(rd(),rd());

	dfs1(1,1);dfs2(1,1);build(root,1,n);

	for(int i = 1;i <= n;++i)ans.insert(0);

	for(int i = 1;i <= m;++i){

		int u,v,w;

		if(getc() == '+'){u = q[i].u = rd();v = q[i].v = rd();w = q[i].w = rd();}

		else{int p = rd();u = q[p].u;v = q[p].v;w = -q[p].w;}

		add(u,v,w);calc(u);calc(v);

		printf("%lld\n",ans.top());

	}

	return 0;

}