Description：

一张 $n$ 个点的完全图，每个点有一个 $c$ 位二进制点权 $x[i]$ ，边 $(u,v)$ 的边权为 $x[u]\text{ xor }x[v]$ ， $q$ 次询问，每次将所有点权 $+\Delta$ 并对 $2^m$ 取模，求最小生成树。

$1\leqslant n,q\leqslant 2\times 10^4,m\leqslant 14$

Solution：

先考虑如果不带修，那么做法是分治，从高到低考虑每一位，将它按这一位划分成两个部分，根据按位贪心的原理这两个部分之间一定只有 $1$ 条边相连，由于数字位的个数限制分治不会超过 $m$ 层，因此复杂度为 $nm$ ，求那一条边可以用 $01trie$ 。

现在的问题是带修，考虑到取模的循环问题，我们可以把原数组倍长，那么每次询问的是数组上一段连续的区间，点权 $+\Delta$ 对应询问区间的左移，因此我们可以考虑用维护区间的数据结构维护他。

因为我们可能会询问任何一个长度为 $2^m$ 的区间，因此我们希望每一个连续的长度为 $2^m$ 的区间都构成一个分治树的结构，我们可以利用 $ST$ 表，也就是对于每个长度为 $2^k$ 的区间都新建一个节点，共 $n\log n$ 个节点，然后每个长度为 $2^m$ 的区间以及后代拿出来就是 $+\Delta$ 之后的分治树，分治最重要的是多个部分信息的合并，考虑如何合并两个子节点的信息，我们可以预处理一个 $a[i][j]$ 表示块 $i$ 和块 $j$ 之间的最小边，那么我们可以从儿子的儿子四个节点的四个跨过中点的连边中选一个最小的，还要考虑这一位的贡献，用图表示就是：

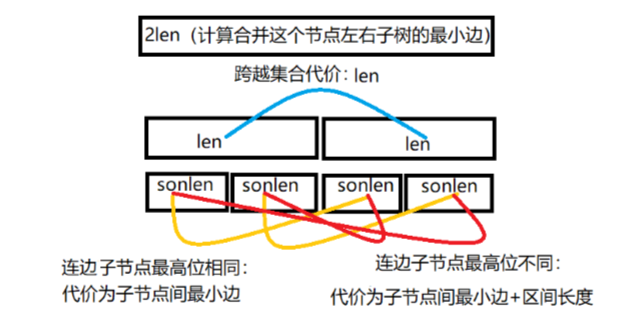
但是这样由于最后叶子节点有 $n$ 个，处理 $a[i][j]$ 空间开不下，因此我们可以预处理一些小块的答案就行了。

Code：

#include<algorithm>

#include<iostream>

#include<cstdlib>

#include<cstdio>

#include<cmath>

#include<cctype>

#include<cstring>

using namespace std;

int n,c,q;

#define MAXN 40010

int x[MAXN];

int v[MAXN];

int f[MAXN][20];

int N;

int MIN_EDGE[256][256];

int MST[65536];

#define INF 0x3f3f3f3f

int calcedge(int x,int y)

{

	if(x == 0 || y == 0)return INF;

	int res = INF;

	for(int i = 0;i < 8;++i)if((x >> i) & 1)

		for(int j = 0;j < 8;++j)if((y >> j) & 1)

			res = min(res,i ^ j);

	return res;

}

int d[20];

int calcmst(int s)

{

	for(int i = 0;i < 16;++i)if((s >> i) & 1)d[i] = INF;

	for(int i = 0;i < 16;++i)if((s >> i) & 1){d[i] = 0;break;}

	int ans = 0;

	while(s)

	{

		int p = -1,dist = INF;

		for(int i = 0;i < 16;++i)if(((s >> i) & 1) && d[i] < dist)p = i,dist = d[i];

		ans += dist;s ^= (1 << p);

		for(int i = 0;i < 16;++i)if(((s >> i) & 1) && (i ^ p) < d[i])d[i] = i ^ p;

	}

	return ans;

}

struct node

{

	int lc,rc,s,ans;

}t[MAXN * 20];

int ptr = 0;

int newnode(){return ++ptr;}

void build(int len)

{

	for(int i = 0;i <= N;++i)if(v[i])t[f[i][0] = newnode()] = (node){0,0,1,-1};

	for(int l = 1,k = 1;k < len;++l,k = k << 1)

	{

		for(int i = 0;i < len - 2 * k + 1;++i)

		{

			int lc = f[i][l - 1],rc = f[i + k][l - 1];

			if(!lc && !rc)continue;

			f[i][l] = newnode();

			t[f[i][l]] = (node){lc,rc,(t[lc].s | (t[rc].s << k)),-1};

		}

	}

	return;

}

int min_edge(int rt1,int rt2,int len)

{

	if(rt1 == 0 || rt2 == 0)return INF;

	if(len == 8)return MIN_EDGE[t[rt1].s][t[rt2].s];

	int res = INF,sonlen = len >> 1;

	res = min(res,min_edge(t[rt1].lc,t[rt2].lc,sonlen));

	res = min(res,min_edge(t[rt1].rc,t[rt2].rc,sonlen));

	if(res != INF)return res;

	res = min(res,min_edge(t[rt1].lc,t[rt2].rc,sonlen) + sonlen);

	res = min(res,min_edge(t[rt1].rc,t[rt2].lc,sonlen) + sonlen);

	return res;

}

int mst(int rt,int len)

{

	if(t[rt].ans != -1)return t[rt].ans;

	if(len <= 16)return t[rt].ans = MST[t[rt].s];

	int sonlen = len >> 1;

	if(t[rt].lc == 0)return mst(t[rt].rc,sonlen);

	if(t[rt].rc == 0)return mst(t[rt].lc,sonlen);

	t[rt].ans = mst(t[rt].lc,sonlen) + mst(t[rt].rc,sonlen);

	t[rt].ans += min_edge(t[rt].lc,t[rt].rc,sonlen) + sonlen;

	return t[rt].ans;

}

int main()

{

	scanf("%d%d",&n,&c);

	for(int i = 1;i <= n;++i)scanf("%d",&x[i]);

	sort(x + 1,x + 1 + n);

	n = unique(x + 1,x + 1 + n) - x - 1;

	for(int i = 1;i <= n;++i)v[x[i]] = 1;

	for(int i = (1 << c);i < (1 << (c + 1));++i)v[i] = v[i - (1 << c)];

	for(int i = 0;i < 256;++i)for(int j = 0;j < 256;++j)MIN_EDGE[i][j] = calcedge(i,j);

	for(int i = 0;i < 65536;++i)MST[i] = calcmst(i);

	N = (1 << (c + 1)) - 1;

	build((1 << c) * 2);

	int delta = 0;

	scanf("%d",&q);

	int v;

	int mod = (1 << c);

	for(int i = 1;i <= q;++i)

	{

		scanf("%d",&v);

		delta = (delta - (v % mod) + mod) % mod;

		printf("%d\n",mst(f[delta][c],(1 << c)));

	}

	return 0;

}