卧薪尝胆,厚积薄发。
多项式相关
卷积
$$
f[k]=\sum_{i\oplus j=k} a[i]\times b[j]
$$
系数表达式
$\to$
频域
点值表达式
$\to$
时域
时域卷积,频域乘积,频域卷积,时域乘积。
$O(Nlog N)$
计算卷积。
快速傅里叶变换
用主
$n$
次复数单位根
$\omega_n^k$
插值。
$$
\omega_n^k=(e^{\frac{2\pi i}{n}})^k=\cos k\frac{2\pi}{n}+i \sin k\frac{2\pi}{n}
$$
消去引理:
$$
\omega_{dn}^{dk}=(e^{\frac{2\pi i}{dn}})^{dk}=(e^{\frac{2\pi i}{n}})^k=\omega_n^k
$$
折半引理:
$$
\omega_n^{k+\frac{n}{2}}=(\cos(\frac{n}{2}\times \frac{2\pi}{n})+i\sin(\frac n 2\times \frac{2\pi} 2))\times \omega_n^k=(\cos\pi+i\sin\text{ }\pi)\times \omega_n^k=-\omega_n^k
$$
求和引理:
$$
\sum_{i=0}^{n-1}(\omega_n^k)^i=0(k\ne0)
$$
对系数奇偶分类
$$
\begin{align}
&A(x)=(a_0+a_2x^2+a_4x^4+⋯+a_{n−2}x^{n−2})+(a_1x+a_3x^3+a_5x^5+⋯+a_{n−1}x^{n−1})\\
&A_1(x)=a_0+a_2x+a_4x^2+⋯+a_{n−2}x^{\frac n 2−1}\\
&A_2(x)=a_1+a_3x+a_5x^2+⋯+a_{n−1}x^{\frac n 2−1}
\end{align}
$$
$k<\frac n 2$
$$
A(\omega_n^k)=A_1((\omega_n^k)^2)+\omega_n^kA_2((\omega_n^k)^2)=A_1(\omega_\frac n 2 ^k)+\omega_n^kA_2(\omega_\frac n 2 ^k)
$$
$k>\frac n 2$
$$
\begin{align}
&A(\omega_n^{k+\frac n 2})\\
=&A_1((\omega_n^{k+\frac n 2})^2)+\omega_n^{k+\frac n 2}A_2((\omega_n^{k+\frac n 2})^2)\\
=&A_1(\omega_n^{2k}\times\omega_n^k)-\omega_n^kA_2(\omega_n^{2k}\times\omega_n^n)\\
=&A_1(\omega_n^{2k})-\omega_n^kA_2(\omega_n^{2k})\\
=&A_1(\omega_\frac n 2^k)-\omega_n^kA_2(\omega_\frac n 2^k)
\end{align}
$$
在外层循环
$i$
,
$F[p]$
表示分成的段中
$\omega_i^k$
在当前这个点插值的值,刚开始是多项式系数,即为
$\omega_1^1$
在各个点插值的值,最后就是点值表达式,即为
$\omega_n^p$
在各个点插值的值。
逆
$FFT$
:
已知
$\omega_n^k$
插值得到的点值表达式
$B$
,求系数表达式
$A$
使得
$A(\omega_n^k)=B_k$
。
用
$-\omega_n^k$
插值:
$$
C_k=\sum_{i=0}^{n-1}B_k(\omega_n^{-k})^i=\sum_{i=0}^{n-1}(\sum_{j=0}^{n-1}A_j(\omega_n^i)^j)(\omega_n^{-k})^i=\sum_{i=0}^{n-1}\sum_{j=0}^{n-1}A_j(\omega_n^{j-k})^i=\sum_{j=0}^{n-1}A_j\sum_{i=0}^{n-1}(\omega_n^{j-k})^i
$$
由求和引理得:当
$k\ne 0$
时:
$$
\sum_{i=0}^{n-1}(\omega_n^k)^i=0
$$
否则:
$$
\begin{align}\sum_{i=0}^{n-1}(\omega_n^k)^i=n\end{align}
$$
所以
$C_k=n\times A_k$
,即
$A_k=C_k/n$
。
#include<algorithm>
#include<iostream>
#include<cstdlib>
#include<cstdio>
#include<cmath>
#include<cstring>
using namespace std;
const double PI = acos(-1);
int n,m;
#define MAXN 3100013
int rev[MAXN];
struct complex
{
double r,i;
complex(double r_ = 0.0,double i_ = 0.0){r = r_;i = i_;}
}a[MAXN],b[MAXN];
complex operator + (complex a,complex b){return complex(a.r + b.r,a.i + b.i);}
complex operator - (complex a,complex b){return complex(a.r - b.r,a.i - b.i);}
complex operator * (complex a,complex b){return complex(a.r * b.r - a.i * b.i,a.r * b.i + a.i * b.r);}
void FFT(complex *f,int l,int type)
{
for(int i = 0;i < l;++i)
{
if(i < rev[i])swap(f[i],f[rev[i]]);
}
for(int i = 2;i <= l;i = i << 1)
{
complex wn(cos(-type * 2 * PI / i),sin(-type * 2 * PI / i));
for(int j = 0;j < l;j += i)
{
complex w(1,0);
for(int k = j;k < j + i / 2;++k)
{
complex u = f[k],t = w * f[k + i / 2];
f[k] = u + t;
f[k + i / 2] = u - t;
w = w * wn;
}
}
}
if(type == -1)
{
for(int i = 0;i < l;++i)
{
f[i].r /= l;
}
}
return;
}
int main()
{
scanf("%d%d",&n,&m);
for(int i = 0;i <= n;++i)scanf("%lf",&a[i].r);
for(int i = 0;i <= m;++i)scanf("%lf",&b[i].r);
int len,l;
for(len = 1,l = 0;len <= n + m;len = len << 1,++l);
for(int i = 0;i < len;++i)rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (l - 1));
FFT(a,len,1);
FFT(b,len,1);
for(int i = 0;i < len;++i)
{
a[i] = a[i] * b[i];
}
FFT(a,len,-1);
for(int i = 0;i <= n + m;++i)
{
printf("%d ",(int)(a[i].r + 0.5));
}
return 0;
}
快速数论变换
计算卷积对
$P=r\times2^k+1$
取模的值。
原根的幂在
$mod\text{ }p$
意义下有循环性质。
将
$g^{\frac{P-1}{n}}$
看作
$e^{-\frac{2\pi i}{n}}$
的等价
设
$\omega_n^k=(g^{\frac{P-1}{n}})^k$
消去引理:
$\omega_{dn}^{dk}=(g^{\frac{P-1}{dn}})^{dk}=(g^{\frac{P-1}{n}})^k=\omega_n^k$
折半引理:
$\omega_n^{k+\frac{n}{2}}=(g^{\frac{P-1}{n}})^{k+\frac n 2}=(g^{\frac{P-1}{n}})^k\times g^{\frac{P-1}{2}}$
由于
$g^{\frac{P-1} 2}\equiv-1(mod\text{ }P)$
$\omega_n^{k+\frac n 2}=-g^{\frac{P-1} 2}=-\omega_n^k$
求和引理:
$\begin{align}\sum_{i=0}^{n-1}(\omega_n^k)^i=\frac{(\omega_n^k)^n-1}{\omega_n^k-1} =\frac{((g^\frac {P-1}{n})^k)^n-1}{(g^{\frac{P-1}{n}})^k-1}=\frac{(g^{P-1})^k-1}{\omega_n^k-1}\end{align}$
由费马小定理得:
$g^{P-1}\equiv1(mod\text{ }P)$
$\begin{align}= \frac{1-1}{\omega_n^k-1}=0\end{align}$
即
$\begin{align}\sum_{i=0}^{n-1}(\omega_n^k)^i=0\end{align}$
于是就和
$FFT$
一样了。
逆
$NTT$
时也应除掉
$n$
,计算一下
$n$
对
$MOD$
的逆元,即
$n^{MOD-2}$
。
#include<algorithm>
#include<iostream>
#include<cstdlib>
#include<cstdio>
#include<cmath>
#include<cstring>
using namespace std;
typedef long long ll;
const ll P = 998244353;
int n,m;
#define MAXN 4000010
ll a[MAXN],b[MAXN];
int rev[MAXN];
ll ww[MAXN << 1],*g = ww + MAXN;
ll power(ll a,ll b)
{
ll res = 1;
while(b > 0)
{
if(b & 1)res = (res * a) % P;
a = (a * a) % P;
b = b >> 1;
}
return res;
}
void NTT(ll *f,int l,int type)
{
for(int i = 0;i < l;++i)
{
if(i < rev[i])swap(f[i],f[rev[i]]);
}
for(int i = 2;i <= l;i = i << 1)
{
ll wn = g[type * l / i];
for(int j = 0;j < l;j += i)
{
ll w = 1;
for(int k = j;k < j + i / 2;++k)
{
ll u = f[k],t = (w * f[k + i / 2]) % P;
f[k] = (u + t) % P;
f[k + i / 2] = (u - t + P) % P;
w = (w * wn) % P;
}
}
}
if(type == -1)
{
ll ni = power(l,P - 2);
for(int i = 0;i < l;++i)
{
f[i] = (f[i] * ni) % P;
}
}
return;
}
int main()
{
scanf("%d%d",&n,&m);
for(int i = 0;i <= n;++i)scanf("%lld",&a[i]);
for(int i = 0;i <= m;++i)scanf("%lld",&b[i]);
int len,l;
for(len = 1,l = 0;len <= n + m;len = len << 1,++l);
for(int i = 0;i < len;++i)rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (l - 1));
g[0] = g[-len] = 1;g[1] = g[1 - len] = power(3,(P - 1) / len);
for(int i = 2;i < len;++i)g[i] = g[i - len] = g[i - 1] * g[1] % P;
NTT(a,len,1);
NTT(b,len,1);
for(int i = 0;i < len;++i)
{
a[i] = a[i] * b[i] % P;
}
NTT(a,len,-1);
for(int i = 0;i <= n + m;++i)printf("%lld ",a[i]);
return 0;
}
多项式求逆
给出
$n-1$
次多项式
$F(x)$
,求一个
$n-1$
次多项式
$G(x)$
使得
$F(x)\times G(x)\equiv 1(mod\ x^n)$
若
$n=1$
,则
$\%x=1$
,那么要求的就是
$F[0]$
的逆元,即
$F[0]^{P-2}$
若
$n>1$
,使用倍增方法。
假设已经求出了
$F(x)G'(x)\equiv1\ (mod\ x^{\lceil \frac n 2\rceil})$
由于
$F(x)G(x)\equiv1(mod\ x^n)$
,则
$F(x)G(x)\equiv 1\ (mod\ x^{\lceil \frac n 2 \rceil})$
两式相减得:
$F(x)(G'(x)-G(x))\equiv 0\ (mod\ x^{\lceil \frac n 2 \rceil})$
由于
$F(x)$
不为
$0$
,则
$G'(x)-G(x)\equiv 0\ (mod\ x^{\lceil\frac n 2\rceil})$
平方,得:
$G'(x)^2+G(x)^2-2G'(x)G(x)\equiv0\ (mod\ x^n)$
为什么模
$x^n$
呢?因为根据卷积的定义,有
$\begin{align}(G'(x)-G(x))^2[i]=\sum_{j=0}^i((G'(x)-G(x))[i]\times(G'(x)-G(x))[j-i])\end{align}$
由于
$i$
和
$j-i$
至少有一项小于
$\lceil\frac n 2\rceil$
,而
$(x^{\lceil\frac n 2\rceil})^2 \ge x^n$
,所以乘完之后为零。
由于
$F(x)G(x)\equiv1\ (mod\ x^n)$
,所以乘上一个
$F(x)$
得:
$F(x)G'(x)^2+G(x)-2G'(x)\equiv0\ (mod\ x^n)$
于是
$G(x)\equiv2G'(x)-F(x)G'(x)^2\ (mod\ x^n)$
#include<algorithm>
#include<iostream>
#include<cstdlib>
#include<cstdio>
#include<cmath>
#include<cstring>
using namespace std;
int n;
#define MAXN 200010
typedef long long ll;
const ll P = 998244353;
ll w[MAXN << 2],*g = w + (MAXN << 1);
ll A[MAXN << 1],B[MAXN << 1],c[MAXN << 1];
int rev[MAXN << 1];
ll power(ll a,ll b)
{
ll res = 1;
while(b > 0)
{
if(b & 1)res = res * a % P;
a = a * a % P;
b = b >> 1;
}
return res;
}
void NTT(ll f[],int l,int type)
{
for(int i = 0;i < l;++i)
if(i < rev[i])
swap(f[i],f[rev[i]]);
for(int i = 2;i <= l;i = i << 1)
{
ll wn = g[type * l / i];
for(int j = 0;j < l;j += i)
{
ll w = 1;
for(int k = j;k < j + i / 2;++k)
{
ll u = f[k],t = w * f[k + i / 2] % P;
f[k] = (u + t) % P;
f[k + i / 2] = (u - t + P) % P;
w = w * wn % P;
}
}
}
if(type == -1)
{
ll ni = power(l,P - 2);
for(int i = 0;i < l;++i)
f[i] = f[i] * ni % P;
}
return;
}
void work(int deg,ll *a,ll *b)
{
if(deg == 1)
{
b[0] = power(a[0],P - 2);
return;
}
work(((deg + 1) >> 1),a,b);
int len,l;
for(len = 1,l = 0;len < (deg << 1);len = len << 1,++l);
for(int i = 1;i < len;++i)rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (l - 1));
g[0] = g[-len] = 1;g[1] = g[1 - len] = power(3,(P - 1) / len);
for(int i = 2;i < len;++i)g[i] = g[i - len] = g[i - 1] * g[1] % P;
for(int i = 0;i < deg;++i)c[i] = a[i];
for(int i = deg;i < len;++i)c[i] = 0;
NTT(b,len,1);NTT(c,len,1);
for(int i = 0;i < len;++i)
{
b[i] = ((2 * b[i] % P) - (c[i] * b[i] % P * b[i] % P) + P) % P;
}
NTT(b,len,-1);
for(int i = deg;i < len;++i)b[i] = 0;
return;
}
int main()
{
scanf("%d",&n);
for(int i = 0;i < n;++i)scanf("%lld",&A[i]);
work(n,A,B);
for(int i = 0;i < n;++i)printf("%lld ",B[i]);
return 0;
}
分治FFT
大概要求的就是给定长度为
$n-1$
的数组
$g[1],g[2],\dots,g[n-1]$
,求
$f[0],f[1],\dots,f[n-1]$
,其中
$$
f[i]=\sum_{j=1}^if[i-j]g[j]
$$
边界为
$f[0]=1$
。答案模
$998244353$
。(洛谷分治FFT模板)
首先可以类似
$cdq$
分治那样的做法,左边的位置对右边的贡献是独立的,假如求出了
$[l,mid]$
的答案,对右边
$x$
位置的贡献为:
$$
w_x=\sum_{i=l}^{mid}f[i]\times g[x-i]
$$
这本质上是个卷积,可以用
$FFT$
加速,时间复杂度
$O(n\log^2n )$
。
但是还有更优秀的做法。
考虑多项式
$F$
,把它写成形式幂级数或者说是生成函数的形式,即:
$$
F(x)=\sum_{i=0}^\infty f[i]x^i
$$
由于
$g_0=0$
,所以有
$F(x)G(x)=F(x)-f_0$
,这个也很好理解,因为卷积的过程就是上面那个式子求的过程,所以自然
$F$
除了最后一位别的都是不变的。
那么就有
$F(x)\equiv(1-G(x))^{-1}(\mod x^n)$
,于是用多项式求逆解决就好了。
#include<algorithm>
#include<iostream>
#include<cstdlib>
#include<cstdio>
#include<cmath>
#include<cctype>
#include<cstring>
using namespace std;
int n;
#define MAXN 400010
#define P 998244353
typedef long long ll;
ll F[MAXN],G[MAXN];
ll ww[MAXN << 1],*g = ww + MAXN;
int rev[MAXN];
ll power(ll a,ll b)
{
ll res = 1;
while(b > 0)
{
if(b & 1)res = res * a % P;
a = a * a % P;
b = b >> 1;
}
return res;
}
void NTT(ll f[],int l,int type)
{
for(int i = 0;i < l;++i)
{
if(i < rev[i])swap(f[i],f[rev[i]]);
}
for(int i = 2;i <= l;i = i << 1)
{
ll wn = g[type * l / i];
for(int j = 0;j < l;j += i)
{
ll w = 1;
for(int k = j;k < j + i / 2;++k)
{
ll u = f[k],t = w * f[k + i / 2] % P;
f[k] = (u + t) % P;
f[k + i / 2] = (u - t + P) % P;
w = w * wn % P;
}
}
}
if(type == -1)
{
for(int i = 0;i < l;++i)f[i] = f[i] * power(l,P - 2) % P;
}
return;
}
ll c[MAXN];
void calc_inv(int deg,ll a[],ll b[])
{
if(deg == 1)
{
b[0] = power(a[0],P - 2) % P;
return;
}
calc_inv((deg + 1) >> 1,a,b);
int l = 0,len = 1;
for(;len < (deg << 1);len = len << 1,++l);
for(int i = 0;i < len;++i)rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (l - 1));
g[0] = g[-len] = 1;g[1] = g[1 - len] = power(3,(P - 1) / len);
for(int i = 2;i < len;++i)g[i] = g[i - len] = g[i - 1] * g[1] % P;
for(int i = 0;i < deg;++i)c[i] = a[i];
for(int i = deg;i < len;++i)c[i] = 0;
NTT(c,len,1);NTT(b,len,1);
for(int i = 0;i < len;++i)
{
b[i] = (2 * b[i] % P - c[i] % P * b[i] % P * b[i] % P + P) % P;
}
NTT(b,len,-1);
for(int i = deg;i < len;++i)b[i] = 0;
return;
}
int main()
{
scanf("%d",&n);
for(int i = 1;i < n;++i)scanf("%lld",&G[i]);
for(int i = 1;i < n;++i)G[i] = P - G[i];
G[0] = (G[0] + 1) % P;
int len;
for(len = 1;len < n;len = len << 1);
calc_inv(len,G,F);
for(int i = 0;i < n;++i)printf("%lld ",F[i]);
cout << endl;
return 0;
}
另一种做法是
$CDQ$
分治,也就是考虑左边对右边的影响,用
$FFT$
加速,注意下标的变化。
#include<algorithm>
#include<iostream>
#include<cstdlib>
#include<cstdio>
#include<cmath>
#include<cctype>
#include<cstring>
using namespace std;
int n;
#define MAXN 400010
typedef long long ll;
ll g[MAXN];
ll f[MAXN];
#define P 998244353
ll power(ll a,ll b)
{
ll res = 1;
while(b > 0)
{
if(b & 1)res = res * a % P;
a = a * a % P;
b = b >> 1;
}
return res;
}
namespace poly
{
int rev[MAXN];
ll ww[MAXN << 1],*g = ww + MAXN;
void NTT(ll f[],int l,int type)
{
for(int i = 0;i < l;++i)
{
if(i < rev[i])swap(f[i],f[rev[i]]);
}
for(int i = 2;i <= l;i = i << 1)
{
ll wn = g[type * l / i];
for(int j = 0;j < l;j += i)
{
ll w = 1;
for(int k = j;k < j + i / 2;++k)
{
ll u = f[k],t = w * f[k + i / 2] % P;
f[k] = (u + t) % P;
f[k + i / 2] = (u - t + P) % P;
w = w * wn % P;
}
}
}
if(type == -1)
{
ll ni = power(l,P - 2);
for(int i = 0;i < l;++i)f[i] = f[i] * ni % P;
}
return;
}
void mul(ll a[],ll b[],ll res[],int deg)
{
int l = 0,len = 1;
for(;len <= (deg << 1);len = len << 1)++l;
g[0] = g[-len] = 1;g[1] = g[1 - len] = power(3,(P - 1) / len);
for(int i = 2;i < len;++i)g[i] = g[i - len] = g[i - 1] * g[1] % P;
for(int i = 0;i < len;++i)rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (l - 1));
NTT(a,len,1);NTT(b,len,1);
for(int i = 0;i < len;++i)res[i] = a[i] * b[i] % P;
NTT(res,len,-1);
for(int i = 0;i < len;++i)a[i] = b[i] = 0;
return;
}
}
ll tmp1[MAXN],tmp2[MAXN],tmp3[MAXN];
void cdq(int l,int r)
{
if(l == r)return;
int mid = ((l + r) >> 1);
cdq(l,mid);
for(int i = l;i <= mid;++i)tmp1[i - l] = f[i];
for(int i = 0;i <= r - l + 1;++i)tmp2[i] = g[i];
int d = r - l + 1 + 1;
poly::mul(tmp1,tmp2,tmp3,d);
for(int i = mid + 1;i <= r;++i)f[i] = (f[i] + tmp3[i - l]) % P;
for(int i = 0;i < d;++i)tmp1[i] = tmp2[i] = tmp3[i] = 0;
cdq(mid + 1,r);
return;
}
int main()
{
scanf("%d",&n);
for(int i = 1;i < n;++i)scanf("%lld",&g[i]);
f[0] = 1;
cdq(0,n);
for(int i = 0;i < n;++i)printf("%lld ",f[i]);
cout << endl;
return 0;
}
多项式除法
给定一个
$n$
次多项式
$F(x)$
和一个
$m$
次多项式
$G(x)$
,请求出多项式
$Q(x)$
,
$R(x)$
,满足以下条件:
$Q(x)$
次数为
$n-m$
,
$R(x)$
次数小于
$m$
,
$F(x) = Q(x) \times G(x) + R(x)$
所有的运算在模
$998244353$
意义下进行。
首先定义多项式的反转,设一个次数界为
$n$
的多项式
$F(x)$
,
$F^R(x)=x^nF(\frac 1 x)$
,因为观察一下就会发现这个实际上是把原多项式高低次数的位置依次交换。
那么我们可以进行这样一个操作,把上面那个式子两边同成
$x^n$
,并把
$\frac 1 x$
当作
$x$
带入,即:
$$
\begin{align}
&x^nF(\frac 1 x)=x^{n-m}Q(\frac 1 x)\times x^mG(\frac 1 x)+x^{n-m+1}x^{m-1}R(\frac 1 x)\\
\Longrightarrow&F^R(x)=Q^R(x)\times G^R(x)+x^{n-m+1}R^R(x)
\end{align}
$$
由于我们最终要求的
$Q(x)$
是一个
$n-m$
次多项式,所以有:
$$
F^R(x)=Q^R(x)\times G^R(x)(\mod x^{n-m+1})
$$
所以
$Q^R=F^R(x)\times (G^R)^{-1}(\mod x^{n-m+1})$
,多项式求逆就可以了。
多项式取模
多项式除法后把
$Q$
带回去解出
$R$
即可。
除了优化递推好像没啥用。
多项式除法和取模的代码:
#include<algorithm>
#include<iostream>
#include<cstdlib>
#include<cstdio>
#include<cmath>
#include<cctype>
#include<cstring>
using namespace std;
int n,m;
#define MAXN 300010
typedef long long ll;
const ll P = 998244353;
ll ww[MAXN << 1],*g = ww + MAXN;
int rev[MAXN];
ll F[MAXN],G[MAXN],Q[MAXN];
ll power(ll a,ll b)
{
ll res = 1;
while(b > 0)
{
if(b & 1)res = res * a % P;
a = a * a % P;
b = b >> 1;
}
return res;
}
void NTT(ll f[],int l,int type)
{
for(int i = 0;i < l;++i)
{
if(i < rev[i])swap(f[i],f[rev[i]]);
}
for(int i = 2;i <= l;i = i << 1)
{
ll wn = g[type * l / i];
for(int j = 0;j < l;j += i)
{
ll w = 1;
for(int k = j;k < j + i / 2;++k)
{
ll u = f[k],t = w * f[k + i / 2] % P;
f[k] = (u + t) % P;
f[k + i / 2] = (u - t + P) % P;
w = w * wn % P;
}
}
}
if(type == -1)
{
ll inv = power(l,P - 2);
for(int i = 0;i < l;++i)f[i] = f[i] * inv % P;
}
return;
}
ll c[MAXN];
void calc_inv(int deg,ll a[],ll b[])
{
if(deg == 1)
{
b[0] = power(a[0],P - 2);
return;
}
calc_inv((deg + 1) >> 1,a,b);
int l = 0,len = 1;
for(;len < (deg << 1);len = len << 1)++l;
for(int i = 0;i < len;++i)rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (l - 1));
g[0] = g[-len] = 1;g[1] = g[1 - len] = power(3,(P - 1) / len);
for(int i = 2;i < len;++i)g[i] = g[i - len] = g[i - 1] * g[1] % P;
for(int i = 0;i < deg;++i)c[i] = a[i];
for(int i = deg;i < len;++i)c[i] = 0;
NTT(c,len,1);NTT(b,len,1);
for(int i = 0;i < len;++i)
{
b[i] = (2 * b[i] % P - c[i] * b[i] % P * b[i] % P + P) % P;
}
NTT(b,len,-1);
for(int i = deg;i < len;++i)b[i] = 0;
return;
}
int main()
{
scanf("%d%d",&n,&m);
for(int i = 0;i <= n;++i)scanf("%lld",&F[n - i]);
for(int i = 0;i <= m;++i)scanf("%lld",&G[m - i]);
calc_inv(n - m + 1,G,Q);
++n;++m;
int l = 0,len = 1;
for(;len < (n << 1);len = len << 1)++l;
for(int i = 0;i < len;++i)rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (l - 1));
g[0] = g[-len] = 1;g[1] = g[1 - len] = power(3,(P - 1) / len);
for(int i = 2;i < len;++i)g[i] = g[i - len] = g[i - 1] * g[1] % P;
NTT(F,len,1);NTT(Q,len,1);
for(int i = 0;i < len;++i)Q[i] = Q[i] * F[i] % P;
NTT(Q,len,-1);NTT(F,len,-1);
for(int i = n - m + 1;i < len;++i)Q[i] = 0;
for(int i = 0,j = n - m;i < j;++i,--j)swap(Q[i],Q[j]);
for(int i = 0;i < n - m + 1;++i)printf("%lld ",Q[i]);puts("");
for(int i = 0,j = n - 1;i < j;++i,--j)swap(F[i],F[j]);
for(int i = 0,j = m - 1;i < j;++i,--j)swap(G[i],G[j]);
l = 0,len = 1;
for(;len < n + 1;len = len << 1)++l;
for(int i = 0;i < len;++i)rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (l - 1));
g[0] = g[-len] = 1;g[1] = g[1 - len] = power(3,(P - 1) / len);
for(int i = 2;i < len;++i)g[i] = g[i - len] = g[i - 1] * g[1] % P;
NTT(G,len,1);NTT(Q,len,1);
for(int i = 0;i < len;++i)Q[i] = Q[i] * G[i] % P;
NTT(Q,len,-1);
for(int i = 0;i < len;++i)F[i] = (F[i] - Q[i] + P) % P;
for(int i = 0;i < m - 1;++i)printf("%d ",F[i]);puts("");
return 0;
}
##多项式牛顿迭代法
假设我们有一个多项式的函数
$G(x)$
,我们想求它的一个零点,换一种方法来说就是求解:
$$
G(F(x))=0(\mod x^n)
$$
首先当
$n=1$
时,
$G(F(x))=0(\mod x)$
,这个需要单独求出。
当
$n\ne 1$
时,假设已经求出了:
$$
G(F_0(x))=0(\mod x^{\lfloor\frac n 2\rfloor})
$$
我们可以把
$G(x)$
在
$F_0(x)$
这里泰勒展开,即:
$$
G(F(x))=G(F_0(x))+\frac{G'(F_0(x))}{1!}(F(x)-F_0(x))+\frac{G''(F_0(x))}{2!}(F(x)-F_0(x))^2+\cdots
$$
由于
$F(x)$
和
$F_0(x)$
最后
$\lfloor\frac n 2\rfloor$
项一定相同,因为他们实际上只是模的东西不一样,本质是一个东西,所以
$(F(x)-F_0(x))^2$
后
$n$
项一定都是
$0$
,于是就可以模掉了,于是有:
$$
G(F(x))=G(F_0(x))+G'(F_0(x))(F(x)-F_0(x))=0(\mod x^n)
$$
于是就有:
$$
F(x)=F_0(x)-\frac{G(F_0(x))}{G'(F_0(x))}
$$
所以如果支持把
$F_0(x)$
快速代入
$G()$
,那么我们就有了一个复杂度为
$T(n)=T(\frac n 2)+O(代入G+n\log n)$
的求解多项式函数
$G(x)$
的零点的做法。
多项式开方
给出多项式
$H(x)$
,要求一个多项式
$F(x)$
满足:
$$
F^2(x)=H(x)(\mod x^n)
$$
做法还是利用牛顿迭代,设函数
$G(x)$
为:
$$
G(F(x))=F^2(x)-H(x)
$$
带入牛顿迭代公式为:
$$
F=F_0-\frac{G(F_0)}{G'(F_0)}=F_0-\frac{F_0^2-H}{2F_0}
$$
时间复杂度
$O(n\log n)$
。
注意当
$deg=0$
的时候要求模意义下的二次剩余,二次剩余有一个叫做
$Cipolla$
的算法,但是如果
$0$
次项的值已知那么就可以在下面把二次剩余枚举得出。
#include<algorithm>
#include<iostream>
#include<cstdlib>
#include<cstdio>
#include<cmath>
#include<cctype>
#include<cstring>
using namespace std;
int n,m;
#define MAXN 400010
int ww[MAXN << 1],*g = ww + MAXN;
int rev[MAXN];
#define P 998244353
int power(int a,int b)
{
int res = 1;
while(b > 0)
{
if(b & 1)res = 1ll * res * a % P;
a = 1ll * a * a % P;
b = b >> 1;
}
return res;
}
void NTT(int f[],int l,int type)
{
for(int i = 0;i < l;++i)
{
if(i < rev[i])swap(f[i],f[rev[i]]);
}
for(int i = 2;i <= l;i = i << 1)
{
int wn = g[type * l / i];
for(int j = 0;j < l;j += i)
{
int w = 1;
for(int k = j;k < j + i / 2;++k)
{
int u = f[k],t = 1ll * w * f[k + i / 2] % P;
f[k] = (u + t) % P;
f[k + i / 2] = (u - t + P) % P;
w = 1ll * w * wn % P;
}
}
}
if(type == -1)
{
int ni = power(l,P - 2);
for(int i = 0;i < l;++i)f[i] = 1ll * f[i] * ni % P;
}
return;
}
int invtmp[MAXN];
void calc_inv(int deg,int a[],int b[])
{
if(deg == 1)
{
b[0] = power(a[0],P - 2);
return;
}
calc_inv((deg + 1) >> 1,a,b);
int l = 0,len = 1;
for(;len <= (deg << 1);len = len << 1)++l;
for(int i = 0;i < len;++i)rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (l - 1));
g[0] = g[-len] = 1;g[1] = g[1 - len] = power(3,(P - 1) / len);
for(int i = 2;i < len;++i)g[i] = g[i - len] = 1ll * g[i - 1] * g[1] % P;
for(int i = 0;i < deg;++i)invtmp[i] = a[i];
for(int i = deg;i < len;++i)invtmp[i] = 0;
NTT(invtmp,len,1);NTT(b,len,1);
for(int i = 0;i < len;++i)
{
b[i] = (2 * b[i] % P - 1ll * invtmp[i] * b[i] % P * b[i] % P + P) % P;
}
NTT(b,len,-1);
for(int i = deg;i < len;++i)b[i] = 0;
//for(int i = 0;i < deg;++i)cout << b[i] * 2 % P << " ";cout << endl;
return;
}
int multmp[MAXN];
void mul(int deg,int a[],int b[])
{
int l = 0,len = 1;
for(;len <= (deg << 1);len = len << 1)++l;
for(int i = 0;i < len;++i)rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (l - 1));
g[0] = g[-len] = 1;g[1] = g[1 - len] = power(3,(P - 1) / len);
for(int i = 2;i < len;++i)g[i] = g[i - len] = 1ll * g[i - 1] * g[1] % P;
for(int i = 0;i < len;++i)multmp[i] = b[i];
NTT(a,len,1);NTT(multmp,len,1);
for(int i = 0;i < len;++i)
{
a[i] = 1ll * a[i] * multmp[i] % P;
}
NTT(a,len,-1);
for(int i = deg;i < len;++i)a[i] = 0;
return;
}
#define REM 1
int tmp1[MAXN],tmp2[MAXN];
void calc_sqr(int deg,int a[],int b[])
{
if(deg == 1)
{
b[0] = REM;
return;
}
calc_sqr((deg + 1) >> 1,a,b);
for(int i = 0;i < deg;++i)tmp1[i] = b[i];
mul(deg,tmp1,b);
for(int i = 0;i < deg;++i)tmp1[i] = (tmp1[i] - a[i] + P) % P;
memset(tmp2,0,sizeof(tmp2));
calc_inv(deg,b,tmp2);
for(int i = 0;i < deg;++i)tmp2[i] = 1ll * tmp2[i] * power(2,P - 2) % P;
mul(deg,tmp1,tmp2);
for(int i = 0;i < deg;++i)b[i] = (b[i] - tmp1[i] + P) % P;
for(int i = 0;i < deg;++i)cout << b[i] << " ";cout << endl;
return;
}
int H[MAXN],F[MAXN];
int main()
{
scanf("%d",&n);
for(int i = 0;i < n;++i)scanf("%d",&H[i]);
calc_sqr(n,H,F);
for(int i = 0;i < n;++i)printf("%d ",F[i]);
cout << endl;
return 0;
}
多项式取模优化常系数齐次线性递推
常系数齐次线性递推,就是给你一个线性递推关系:
$$
f_n=\sum_{i=1}^ka_if_{n-i}
$$
让你求第
$n$
项的值。
显然可以矩阵乘法,但是矩阵乘法复杂度是
$O(k^3\log n)$
,不难发现复杂度的瓶颈主要在
$k^3$
这部分,因为对于绝大多数问题,
$\log n$
都比较小。
特征多项式:
特征值,特征向量:
如果有一个常数
$\lambda$
和一个向量
$\overrightarrow v$
,满足
$\lambda\overrightarrow v=A\overrightarrow v$
,则称
$\overrightarrow v$
为矩阵
$A$
的一组特征向量,
$\lambda$
为矩阵
$A$
的一组特征值。
秩为
$k$
的矩阵有
$k$
组线性不相关的特征向量。
特征多项式,特征方程:
对关系式进行变换:
$(\lambda I-A)\overrightarrow v=0$
,这个等式有解的充要条件是
$\det(\lambda I-A)=0$
,那么我们可以把
$\det(\lambda I-A)$
看作一个
$k$
次多项式,记为:
$f(\lambda)=\det(\lambda I-A)$
,这个称为矩阵的特征多项式,
$f(\lambda)$
称为矩阵的特征方程,这个方程有
$k$
个解可以写作:
$$
f(\lambda)=\prod_{i=1}^k(\lambda_i-\lambda)
$$
每个解是一个特征值。
Cayley-Hamilton定理:
根据:Cayley-Hamilton定理,有
$f(A)=0$
,证明的话:
$$
\begin{align}
&f(A)=\prod_{i=1}^k(\lambda_iI-A)\\
&首先有:(\lambda_iI-A)\times(\lambda_j I-A)=\lambda_i\lambda_jI^2-(\lambda_i+\lambda_j)IA+A^2=(\lambda_jI-A)\times(\lambda_i I-A)\\
&我们只要证明f(A)乘任何特征向量都会得到0矩阵,就可以说明矩阵A=0\\
&f(A)\times \overrightarrow {v_i}=\prod_{j\ne i}(\lambda_jI-A)(\lambda_i I-A)\overrightarrow {v_i}=\prod_{j\ne i}(\lambda_jI-A)\times 0=0\\
&\therefore f(A)=0
\end{align}
$$
优化递推:
设转移矩阵为
$M$
,根据矩阵快速幂,我们只要能求出来
$M^n$
就行了。
$x^n$
可以看作一个
$n$
次多项式,那么我们用
$f(x)$
来表示就是
$x^n=f(x)\times g(x)+h(x)$
。
即
$M^n=f(M)\times g(M)+h(M)$
,但是由于
$f(M)=0$
,因此:
$M^n=h(M)$
,于是我们可以倍增:也就是每次
$H(n)=h(n)\times h(n)$
,但是
$H(n)$
是
$2k-2$
次的,因此我们可以手动多项式取模,复杂度
$O(k^2\log n)$
,如果用
$FFT$
卷积
$+$
多项式除法可以做到
$O(k\log k\log n)$
。
还有一个问题,就是
$f(x)$
怎么求,手动模拟一下求行列式的过程会发现
$[x^i]f(x)=-a[k-i],[x^k]f(x)=1$
。
总之当个板子记住就行了。
Code:
暴力取模:
#include<algorithm>
#include<iostream>
#include<cstdlib>
#include<cstdio>
#include<cmath>
#include<cctype>
#include<cstring>
using namespace std;
int n,k;
#define MAXK 4010
#define MOD 1000000007
inline int rd()
{
register int res = 0,f = 1;register char c = getchar();
while(!isdigit(c)){if(c == '-')f = -1;c = getchar();}
while(isdigit(c))res = (res << 1) + (res << 3) + c - '0',c = getchar();
return res * f;
}
int f[MAXK],h[MAXK];
struct poly
{
int a[MAXK];
poly(){memset(a,0,sizeof(a));}
int& operator [](const int &i){return a[i];}
int operator [](const int &i)const{return a[i];}
inline poly operator * (const poly &b)
{
poly res;
for(register int i = 0;i < k;++i)
for(register int j = 0;j < k;++j)
(res[i + j] += 1ll * a[i] * b[j] % MOD) %= MOD;
for(register int i = 2 * k - 2;i >= k;res[i--] = 0)
for(register int j = 1;j <= k;++j)
(res[i - j] += 1ll * res[i] * f[j] % MOD) %= MOD;
return res;
}
}m;
poly power(poly a,int b)
{
register poly res;
res[0] = 1;
while(b > 0)
{
if(b & 1)res = res * a;
a = a * a;
b = b >> 1;
}
return res;
}
int main()
{
scanf("%d%d",&n,&k);
for(register int i = 1;i <= k;++i)f[i] = rd(),f[i] = (f[i] > 0 ? f[i] : f[i] + MOD);
for(register int i = 0;i < k;++i)h[i] = rd(),h[i] = (h[i] > 0 ? h[i] : h[i] + MOD);
if(n < k){cout << h[n] << endl;return 0;}
m[1] = 1;int ans = 0;
m = power(m,n);
for(register int i = 0;i < k;++i)(ans += 1ll * m[i] * h[i] % MOD) %= MOD;
cout << ans << endl;
return 0;
}
$FFT$
卷积
$+$
多项式取模:
#include<algorithm>
#include<iostream>
#include<cstdlib>
#include<cstdio>
#include<cmath>
#include<cctype>
#include<cstring>
using namespace std;
int n,k;
#define MAXK 248000
#define MOD 998244353
inline int rd()
{
register int res = 0,f = 1;register char c = getchar();
while(!isdigit(c)){if(c == '-')f = -1;c = getchar();}
while(isdigit(c))res = (res << 1) + (res << 3) + c - '0',c = getchar();
return res * f;
}
int f_[MAXK],h[MAXK];
namespace polynomial
{
int rev[MAXK];
int ww[MAXK << 1],*g = ww + MAXK;
int power(int a,int b)
{
int res = 1;
while(b > 0)
{
if(b & 1)res = 1ll * res * a % MOD;
a = 1ll * a * a % MOD;
b = b >> 1;
}
return res;
}
int init(int n)
{
int l = 0,len = 1;
for(;len <= n;len = len << 1)++l;
for(int i = 0;i < len;++i)rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (l - 1));
g[0] = g[-len] = 1;g[1] = g[1 - len] = power(3,(MOD - 1) / len);
for(int i = 2;i < len;++i)g[i] = g[i - len] = 1ll * g[i - 1] * g[1] % MOD;
return len;
}
struct poly
{
int a[MAXK];
int d;
poly(){memset(a,0,sizeof(a));d = 0;}
int& operator [](int x){return a[x];}
int operator [](int x)const{return a[x];}
};
void NTT(poly &f,int l,int type)
{
for(int i = 0;i < l;++i)
{
if(i < rev[i])swap(f[i],f[rev[i]]);
}
for(int i = 2;i <= l;i = i << 1)
{
int wn = g[type * l / i];
for(int j = 0;j < l;j += i)
{
int w = 1;
for(int k = j;k < j + i / 2;++k)
{
int u = f[k],t = 1ll * w * f[k + i / 2] % MOD;
f[k] = (u + t) % MOD;
f[k + i / 2] = (u - t + MOD) % MOD;
w = 1ll * w * wn % MOD;
}
}
}
if(type == -1)
{
int ni = power(l,MOD - 2);
for(int i = 0;i < l;++i)f[i] = 1ll * f[i] * ni % MOD;
}
return;
}
poly operator * (poly a,poly b)
{
poly res;
int len = init(a.d + b.d);res.d = a.d + b.d;
NTT(a,len,1);NTT(b,len,1);
for(int i = 0;i < len;++i)res[i] = 1ll * a[i] * b[i] % MOD;
NTT(res,len,-1);
return res;
}
poly invtmp;
void calc_inv(poly &a,poly &b,int deg)
{
if(deg == 1){b[0] = power(a[0],MOD - 2);return;}
calc_inv(a,b,((deg + 1) >> 1));
int len = init(deg << 1);
for(int i = 0;i < deg;++i)invtmp[i] = a[i];
for(int i = deg;i < len;++i)invtmp[i] = 0;
NTT(invtmp,len,1);NTT(b,len,1);
for(int i = 0;i < len;++i)
{
b[i] = (2ll * b[i] % MOD - 1ll * invtmp[i] * b[i] % MOD * b[i] % MOD + MOD) % MOD;
}
NTT(b,len,-1);
for(int i = deg;i < len;++i)b[i] = 0;
b.d = deg - 1;
return;
}
poly operator + (poly a,poly b)
{
poly res;
res.d = max(a.d,b.d);
for(int i = 0;i < res.d;++i)res[i] = (a[i] + b[i]) % MOD;
return res;
}
poly operator - (poly a,poly b)
{
poly res;
res.d = max(a.d,b.d);
for(int i = 0;i < res.d;++i)res[i] = (a[i] - b[i] + MOD) % MOD;
return res;
}
poly divtmp;
poly operator / (poly a,poly b)
{
for(int i = 0;i <= divtmp.d;++i)divtmp[i] = 0;
for(int i = 0,j = a.d;i < j;++i,--j)swap(a[i],a[j]);
for(int i = 0,j = b.d;i < j;++i,--j)swap(b[i],b[j]);
calc_inv(b,divtmp,b.d + 1);
divtmp = divtmp * a;
for(int i = a.d - b.d + 1;i <= divtmp.d;++i)divtmp[i] = 0;
divtmp.d = a.d - b.d;
for(int i = 0,j = divtmp.d;i < j;++i,--j)swap(divtmp[i],divtmp[j]);
return divtmp;
}
poly operator % (poly a,poly b)
{
poly res = a - a / b * b;
res.d = b.d - 1;
return res;
}
}
using namespace polynomial;
poly f;
struct matrix
{
poly a;
int& operator [](int x){return a[x];}
int operator [](int x)const{return a[x];}
friend inline matrix operator * (matrix a,matrix b)
{
matrix res;
res.a = a.a * b.a;
res.a = res.a % f;
return res;
}
}m;
matrix power(matrix a,int b)
{
matrix res;
res[0] = 1;
while(b > 0)
{
if(b & 1)res = res * a;
a = a * a;
b = b >> 1;
}
return res;
}
int main()
{
scanf("%d%d",&n,&k);
for(register int i = 1;i <= k;++i)f_[i] = rd(),f_[i] = (f_[i] > 0 ? f_[i] : f_[i] + MOD);
for(register int i = 0;i < k;++i)h[i] = rd(),h[i] = (h[i] > 0 ? h[i] : h[i] + MOD);
if(n < k){cout << h[n] << endl;return 0;}
f[k] = 1;
for(int i = 0;i < k;++i)f[i] = MOD - f_[k - i];
f.d = k;
m[1] = 1;m.a.d = k - 1;int ans = 0;
m = power(m,n);
ans = 0;
for(int i = 0;i < k;++i)(ans += 1ll * m[i] * h[i] % MOD) %= MOD;
cout << ans << endl;
return 0;
}
多项式多点求值
多项式快速插值
多项式辗转相除法
多项式求导和积分
求导:
$$
(x^a)'=ax^{a-1}
$$
for(int i = 1;i < n;++i)f[i - 1] = 1ll * i * f[i] % P;
f[n - 1] = 0;
不定积分:
$$
\int^x_0 t^adt=\frac1{a+1}x^{a+1}
$$
for(int i = n - 1;i >= 1;--i)f[i] = 1ll * f[i - 1] * power(i,P - 2) % P;
多项式对数函数
求
$g(x)=\ln f(x)$
。
对两边同时求导,得:
$$
g'(x)=(\ln f(x))'=\ln'f(x)f'(x)=\frac{f'(x)}{f(x)}
$$
所以就先对
$f$
求导除以
$f$
的逆然后再不定积分就可以了。
#include<algorithm>
#include<iostream>
#include<cstdlib>
#include<cstdio>
#include<cmath>
#include<cctype>
#include<cstring>
using namespace std;
int n;
#define MAXN 400010
int f[MAXN],f_[MAXN];
#define P 998244353
int ww[MAXN << 1],*g = ww + MAXN;
int rev[MAXN];
int a[MAXN],b[MAXN],c[MAXN];
int power(int a,int b)
{
int res = 1;
while(b > 0)
{
if(b & 1)res = 1ll * res * a % P;
a = 1ll * a * a % P;
b = b >> 1;
}
return res;
}
void NTT(int f[],int l,int type)
{
for(int i = 0;i < l;++i)
{
if(i < rev[i])swap(f[i],f[rev[i]]);
}
for(int i = 2;i <= l;i = i << 1)
{
int wn = g[type * l / i];
for(int j = 0;j < l;j += i)
{
int w = 1;
for(int k = j;k < j + i / 2;++k)
{
int u = f[k],t = 1ll * w * f[k + i / 2] % P;
f[k] = (u + t) % P;
f[k + i / 2] = (u - t + P) % P;
w = 1ll * w * wn % P;
}
}
}
if(type == -1)
{
int ni = power(l,P - 2);
for(int i = 0;i < l;++i)f[i] = 1ll * f[i] * ni % P;
}
return;
}
void calc_inv(int deg,int a[],int b[])
{
if(deg == 1)
{
b[0] = power(a[0],P - 2);
return;
}
calc_inv((deg + 1) >> 1,a,b);
int l = 0,len = 1;
for(;len < (deg << 1);len = len << 1,++l);
for(int i = 0;i < len;++i)rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (l - 1));
g[0] = g[-len] = 1;g[1] = g[1 - len] = power(3,(P - 1) / len);
for(int i = 2;i <= len;++i)g[i] = g[i - len] = 1ll * g[i - 1] * g[1] % P;
for(int i = 0;i < deg;++i)c[i] = a[i];
for(int i = deg;i < len;++i)c[i] = 0;
NTT(c,len,1);NTT(b,len,1);
for(int i = 0;i < len;++i)
{
b[i] = (2 * b[i] % P - 1ll * c[i] * b[i] % P * b[i] % P + P) % P;
}
NTT(b,len,-1);
for(int i = deg;i < len;++i)b[i] = 0;
return;
}
int main()
{
scanf("%d",&n);
for(int i = 0;i < n;++i)scanf("%d",&f[i]);
calc_inv(n,f,f_);
//for(int i = 0;i < n;++i)cout << f_[i] << " ";cout << endl;
for(int i = 1;i < n;++i)f[i - 1] = 1ll * i * f[i] % P;
//for(int i = 0;i < n;++i)cout << f[i] << " ";cout << endl;
f[n - 1] = 0;
int l = 0,len = 1;
for(;len <= (n << 1);len = len << 1)++l;
for(int i = 0;i < len;++i)rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (l - 1));
g[0] = g[-len] = 1;g[1] = g[1 - len] = power(3,(P - 1) / len);
for(int i = 2;i < len;++i)g[i] = g[i - len] = 1ll * g[i - 1] * g[1] % P;
NTT(f,len,1);NTT(f_,len,1);
for(int i = 0;i < len;++i)f[i] = 1ll * f[i] * f_[i] % P;
NTT(f,len,-1);
for(int i = n - 1;i >= 1;--i)f[i] = 1ll * f[i - 1] * power(i,P - 2) % P;
f[0] = 0;
for(int i = 0;i < n;++i)printf("%d ",f[i]);cout << endl;
return 0;
}
多项式指数函数
要求:
$$
F(x)=e^{H(x)}
$$
两边取对数:
$$
\ln(F(x))-H(x)=0
$$
设
$G(F(x))=\ln(F(x))-H(x)$
根据牛顿迭代有:
$$
F(x)=F_0(x)-\frac{G(F_0(x))}{G'(F_0(x))}
$$
在这里
$H(x)$
其实就是常数项,于是:
$$
G'(F(x))=\frac{1}{F(x)}
$$
那么也就是说:
$$
\begin{align}
F(x)&=F_0(x)-\frac{G(F_0(x))}{G'(F_0(x))}\\
&=F_0(x)-(\ln(F_0(x))+H(x))F_0(x)\\
&=F_0(x)(1-\ln(F_0(x))+H(x))
\end{align}
$$
于是多项式求对数就行了。
#include<algorithm>
#include<iostream>
#include<cstdlib>
#include<cstdio>
#include<cmath>
#include<cctype>
#include<cstring>
using namespace std;
int n;
#define MAXN 800010
typedef long long ll;
ll h[MAXN];
#define P 998244353
ll power(ll a,ll b)
{
ll res = 1;
while(b > 0)
{
if(b & 1)res = res * a % P;
a = a * a % P;
b = b >> 1;
}
return res;
}
void diff(int deg,ll a[],ll b[])
{
memset(b,0,sizeof(b));
for(int i = 1;i < deg;++i)b[i - 1] = i * a[i] % P;
return;
}
void inte(int deg,ll a[],ll b[])
{
memset(b,0,sizeof(b));
for(int i = deg - 1;i >= 1;--i)b[i] = a[i - 1] * power(i,P - 2) % P;
return;
}
ll ww[MAXN << 1],*g = ww + MAXN;
int rev[MAXN];
ll invtmp[MAXN];
void NTT(ll f[],int l,int type)
{
for(int i = 0;i < l;++i)
{
if(i < rev[i])swap(f[i],f[rev[i]]);
}
for(int i = 2;i <= l;i = i << 1)
{
ll wn = g[type * l / i];
for(int j = 0;j < l;j += i)
{
ll w = 1;
for(int k = j;k < j + i / 2;++k)
{
ll u = f[k],t = w * f[k + i / 2] % P;
f[k] = (u + t) % P;
f[k + i / 2] = (u - t + P) % P;
w = w * wn % P;
}
}
}
if(type == -1)
{
ll ni = power(l,P - 2);
for(int i = 0;i < l;++i)f[i] = f[i] * ni % P;
}
return;
}
void calc_inv(int deg,ll a[],ll b[])
{
if(deg == 1)
{
b[0] = power(a[0],P - 2);
return;
}
calc_inv((deg + 1) >> 1,a,b);
int l = 0,len = 1;
for(;len <= (deg << 1);len = len << 1)++l;
for(int i = 0;i < len;++i)rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (l - 1));
g[0] = g[-len] = 1;g[1] = g[1 - len] = power(3,(P - 1) / len);
for(int i = 2;i < len;++i)g[i] = g[i - len] = 1ll * g[i - 1] * g[1] % P;
for(int i = 0;i < deg;++i)invtmp[i] = a[i];
for(int i = deg;i < len;++i)invtmp[i] = 0;
NTT(invtmp,len,1);NTT(b,len,1);
for(int i = 0;i < len;++i)
{
b[i] = ((2 * b[i] % P) - (invtmp[i] * b[i] % P * b[i] % P) + P) % P;
}
NTT(b,len,-1);
for(int i = deg;i < len;++i)b[i] = 0;
return;
}
ll f_[MAXN];
void mul(int deg,ll a[],ll b[])
{
int l = 0,len = 1;
for(;len <= (deg << 1);len = len << 1)++l;
for(int i = 0;i < len;++i)rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (l - 1));
g[0] = g[-len] = 1;g[1] = g[1 - len] = power(3,(P - 1) / len);
for(int i = 2;i < len;++i)g[i] = g[i - len] = 1ll * g[i - 1] * g[1] % P;
NTT(a,len,1);NTT(b,len,1);
for(int i = 0;i < len;++i)
{
a[i] = a[i] * b[i] % P;
}
NTT(a,len,-1);NTT(b,len,-1);
return;
}
ll lntmp[MAXN];
void calc_ln(int deg,ll a[],ll b[])
{
diff(deg,a,f_);
memset(lntmp,0,sizeof(lntmp));
calc_inv(deg,a,lntmp);
mul(deg,f_,lntmp);
inte(deg,f_,b);
return;
}
ll res[MAXN];
ll exptmp[MAXN];
void calc_exp(int deg,ll a[],ll b[])
{
if(deg == 1)
{
b[0] = 1;
return;
}
calc_exp((deg + 1) >> 1,a,b);
calc_ln(deg,b,exptmp);
for(int i = 0;i < deg;++i)exptmp[i] = (a[i] - exptmp[i] + P) % P;
exptmp[0] = (exptmp[0] + 1) % P;
mul(deg,b,exptmp);
return;
}
int main()
{
scanf("%d",&n);
for(int i = 0;i < n;++i)scanf("%lld",&h[i]);
calc_exp(n << 1,h,res);
for(int i = 0;i < n;++i)printf("%lld ",res[i]);cout << endl;
return 0;
}
多项式快速幂
显然可以暴力倍增,但是这样的复杂度是
$O(n\log^2n)$
的,我们希望找到更优秀的做法。
$$
F^k=\exp(k\ln F)
$$
于是先求
$\ln$
乘个
$k$
再
$\exp$
回去就行了。
#include<algorithm>
#include<iostream>
#include<cstdlib>
#include<cstdio>
#include<cmath>
#include<cctype>
#include<cstring>
using namespace std;
int n,s;
#define MAXN 400010
#define P 998244353
#define G 3
int a[MAXN],b[MAXN],c[MAXN];
#define I inline
#define R register
int rev[MAXN];
int ww[MAXN << 1],*g = ww + MAXN;
int power(int a,int b)
{
int res = 1;
for(;b > 0;a = 1ll * a * a % P,b = b >> 1)if(b & 1)res = 1ll * res * a % P;
return res;
}
int inver(int a){return power(a,P - 2);}
int init(int n)
{
int l = 0,len = 1;
for(;len <= n;len = len << 1)++l;
for(int i = 0;i < len;++i)rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (l - 1));
g[0] = g[-len] = 1;g[1] = g[1 - len] = power(G,(P - 1) / len);
for(int i = 2;i < len;++i)g[i] = g[i - len] = 1ll * g[i - 1] * g[1] % P;
return len;
}
void NTT(int f[],int l,int type)
{
for(int i = 0;i < l;++i)
{
if(i < rev[i])swap(f[i],f[rev[i]]);
}
for(int i = 2;i <= l;i = i << 1)
{
int wn = g[type * l / i];
for(int j = 0;j < l;j += i)
{
int w = 1;
for(int k = j;k < j + i / 2;++k)
{
int u = f[k],t = 1ll * w * f[k + i / 2] % P;
f[k] = (u + t) % P;
f[k + i / 2] = (u - t + P) % P;
w = 1ll * w * wn % P;
}
}
}
if(type == -1)
{
int ni = power(l,P - 2);
for(int i = 0;i < l;++i)f[i] = 1ll * f[i] * ni % P;
}
return;
}
int invtmp[MAXN];
void calc_inv(int deg,int a[],int b[])
{
if(deg == 1)
{
b[0] = power(a[0],P - 2);
return;
}
calc_inv(((deg + 1) >> 1),a,b);
int len = init(deg * 2);
for(int i = 0;i < deg;++i)invtmp[i] = a[i];
for(int i = deg;i < len;++i)invtmp[i] = 0;
NTT(invtmp,len,1);NTT(b,len,1);
for(int i = 0;i < len;++i)
{
b[i] = (2ll * b[i] - 1ll * invtmp[i] * b[i] % P * b[i] % P + P) % P;
}
NTT(b,len,-1);
for(int i = deg;i < len;++i)b[i] = 0;
return;
}
int lnt[MAXN];
void poly_ln(int deg,int a[],int b[])
{
calc_inv(deg,a,b);
for(int i = 0;i < deg;++i)lnt[i] = a[i];
for(int i = 0;i < deg;++i)lnt[i] = 1ll * (i + 1) * lnt[i + 1] % P;
int l = init(deg * 2);
NTT(lnt,l,1);NTT(b,l,1);
for(int i = 0;i < l;++i)lnt[i] = 1ll * lnt[i] * b[i] % P;
NTT(lnt,l,-1);
for(int i = deg;i > 0;--i)lnt[i] = 1ll * inver(i) * lnt[i - 1] % P;lnt[0] = 0;
for(int i = 0;i < deg;++i)b[i] = lnt[i];
for(int i = deg;i < l;++i)b[i] = 0;
for(int i = 0;i < l;++i)lnt[i] = 0;
return;
}
int expt[MAXN];
void poly_exp(int deg,int a[],int b[])
{
if(deg == 1)
{
b[0] = 1;
return;
}
poly_exp((deg + 1) >> 1,a,b);
poly_ln(deg,b,expt);
for(int i = 0;i < deg;++i)expt[i] = (a[i] - expt[i] + P) % P;
expt[0] = (expt[0] + 1) % P;
int l = init(deg * 2);
NTT(expt,l,1);NTT(b,l,1);
for(int i = 0;i < l;++i)expt[i] = 1ll * expt[i] * b[i] % P;
NTT(expt,l,-1);
for(int i = 0;i < deg;++i)b[i] = expt[i];
for(int i = deg;i < l;++i)b[i] = 0;
for(int i = 0;i < l;++i)expt[i] = 0;
return;
}
int rd()
{
register int res = 0;register char c = getchar();
while(!isdigit(c))c = getchar();
while(isdigit(c))res = (10ll * res % P + c - '0') % P,c = getchar();
return res;
}
int main()
{
scanf("%d",&n);
s = rd();
for(int i = 0;i < n;++i)scanf("%d",&a[i]);
poly_ln(n,a,b);
for(int i = 0;i < n;++i)b[i] = 1ll * b[i] * s % P;
poly_exp(n,b,c);
for(int i = 0;i < n;++i)printf("%d ",c[i]);
return 0;
}
多项式三角函数
多项式求复合逆
复合逆:如果两个多项式
$F(x)$
和
$G(x)$
满足都没有常数项且一次项系数互为逆元,并且:
$F(G(x))=x$
那么称
$F(x)$
为
$G(x)$
的复合逆,并且一定满足
$F(G(x))=G(F(x))$
。
求复合逆没有
$O(n\log n)$
求
$[1,n]$
的值的方法,但是我们可以
$O(n\log n)$
的求出单点的值:
$$
[x^n]F(x)=\frac1n[x^{n-1}](\frac x{G(x)})^n
$$
这个又称为拉格朗日反演。
另外一个扩展拉格朗日反演:
$$
[x^n]H(F(x))=\frac1nH'(x)(\frac xG(x))^n
$$
所以只用多项式
$\ln+\exp$
即可。
任意模数FFT
任意模数FFT有两种写法,其中第一种常数大,因此我们在此只考虑第二种写法。
首先如果最初的数
$\in[0,N]$
,那么
$FFT$
之后的数不会超过
$N^3$
,考虑卷积的式子就行了。
设模数为
$M$
,设
$M_o=\sqrt M$
,那么我们可以将参与卷积的所有整数表示为
$x=a[x]M_0+b[x]$
,其中
$a[x]$
和
$b[x]$
都是整数,那么可以发现:
$$
x\times y=(a[x]M_0+b[x])\times (a[y]M_0+b[y])=a[x]a[y]M_0^2+a[x]b[y]M_0+a[y]b[x]M_0+b[x]b[y]
$$
也就是说:
$$
\begin{align}
&\sum_{i=0}^nx[i]\times y[n-i]\\
=&M_0^2\sum_{i=0}^na[x[i]]a[y[n-i]]+M_0\sum_{i=0}^na[x[i]]b[y[n-i]]+M_0\sum_{i=0}^na[y[n-i]]b[x[i]]+\sum_{i=0}^nb[x[i]]b[y[n-i]]\\
\end{align}
$$
发现这其实就是四个卷积,所以我们可以分开做,对应系数相同的合在一起
$IDFT$
,一共需要
$4$
次
$DFT$
和
$3$
次
$IDFT$
,一共七次。
可以用一种奇技淫巧优化成4次。
struct comp
{
long double r,i;
comp(long double r_ = 0,long double i_ = 0){r = r_;i = i_;}
};
I comp operator + (comp a,comp b){return comp(a.r + b.r,a.i + b.i);}
I comp operator - (comp a,comp b){return comp(a.r - b.r,a.i - b.i);}
I comp operator * (comp a,comp b){return comp(a.r * b.r - a.i * b.i,a.r * b.i + a.i * b.r);}
int rev[MAXN];
I int init(int n)
{
R int l = 0,len = 1;
for(;len <= n;len = len << 1)++l;
for(R int i = 0;i < len;++i)rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (l - 1));
return len;
}
const long double PI = acos(-1);
I void FFT(comp f[],int l)
{
for(R int i = 0;i < l;++i)
{
if(i < rev[i])swap(f[i],f[rev[i]]);
}
for(R int i = 2;i <= l;i = i << 1)
{
comp wn = comp(cos(PI * 2 / i),sin(PI * 2 / i));
for(R int j = 0;j < l;j += i)
{
comp w = comp(1,0);
for(R int k = j;k < j + i / 2;++k)
{
comp u = f[k],t = w * f[k + i / 2];
f[k] = u + t;
f[k + i / 2] = u - t;
w = w * wn;
}
}
}
return;
}
comp a[MAXN],b[MAXN];
comp r1[MAXN],r2[MAXN],r3[MAXN],r4[MAXN];
typedef long long ll;
comp conj(comp k){return comp(k.r,-k.i);}
I void mul(int x[],int y[],int r[],int l)
{
for(R int i = 0;i < l;++i)a[i] = comp(x[i] & 32767,x[i] >> 15);
for(R int i = 0;i < l;++i)b[i] = comp(y[i] & 32767,y[i] >> 15);
FFT(a,l);FFT(b,l);
for(int i = 0;i < l;++i)
{
int j = (l - i) & (l - 1);
comp da,db,dc,dd;
da = (a[i] + conj(a[j])) * comp(0.5,0);
db = (a[i] - conj(a[j])) * comp(0,-0.5);
dc = (b[i] + conj(b[j])) * comp(0.5,0);
dd = (b[i] - conj(b[j])) * comp(0,-0.5);
r1[j] = da * dc;
r2[j] = da * dd;
r3[j] = db * dc;
r4[j] = db * dd;
}
for(int i = 0;i < l;++i)a[i] = r1[i] + r2[i] * comp(0,1);
for(int i = 0;i < l;++i)b[i] = r3[i] + r4[i] * comp(0,1);
FFT(a,l);FFT(b,l);
for(int i = 0;i < l;++i)
{
int da = (ll)(a[i].r / l + 0.5) % p;
int db = (ll)(a[i].i / l + 0.5) % p;
int dc = (ll)(b[i].r / l + 0.5) % p;
int dd = (ll)(b[i].i / l + 0.5) % p;
r[i] = (da + ((ll)(db + dc) << 15) + ((ll)dd << 30)) % p;
}
return;
}
快速莫比乌斯变换
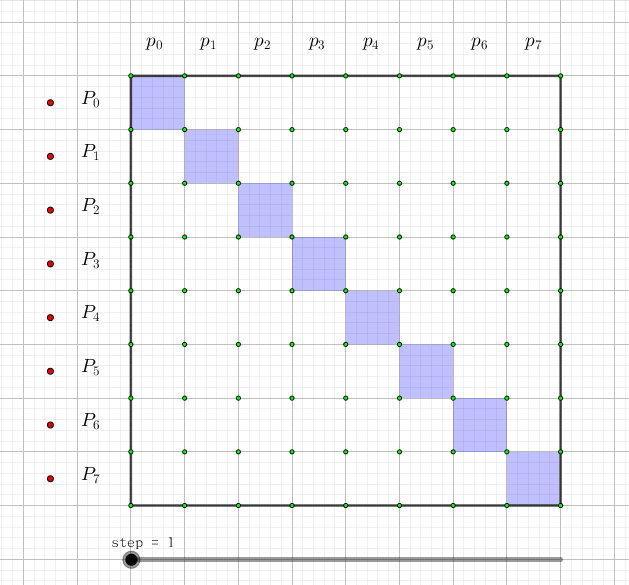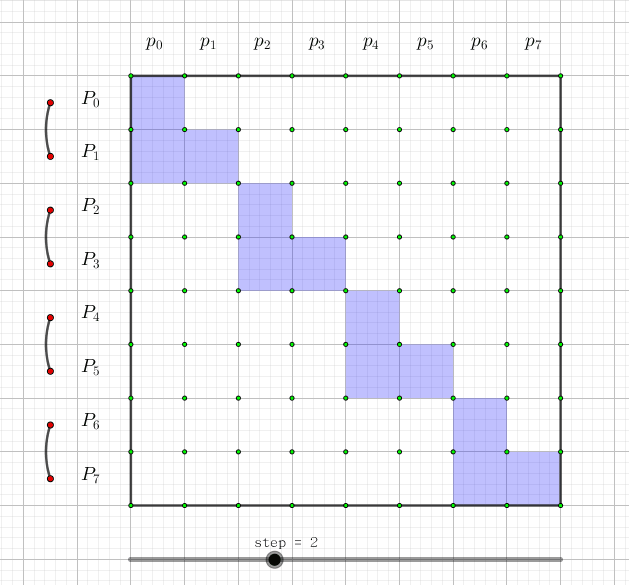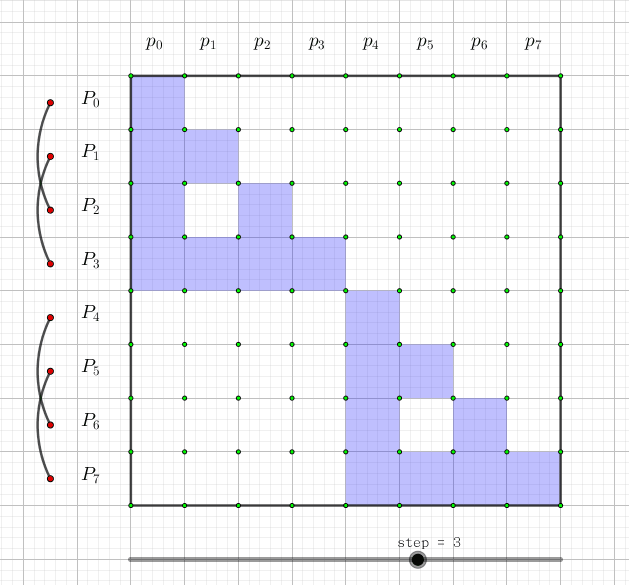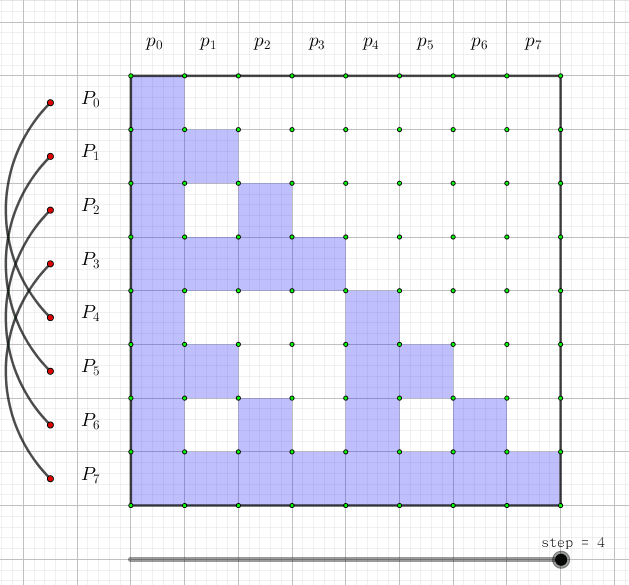
快速莫比乌斯变换是用来解决集合幂级数的集合并卷积的问题,也就是说,给定两个长度为
$2^n-1$
的序列
$a$
和
$b$
,让求一个序列
$c$
满足:
$$
c[k]=\sum_{i\text{ or }j=k}a[i]\times b[j]
$$
暴力做肯定是
$O((2^n)^2)$
的,考虑怎么优化,
$i\cup j=k$
这个很不好处理,那么我们可以做一个集合的前缀和(用大写字母表示):
$$
\begin{align}
C[k]&=\sum_{k_0\subseteq k}c[k_0]\\
&=\sum_{k_0\subseteq k}\sum_{i\cup j=k_0}a[i]\times b[j]\\
&=\sum_{i\cup j\subseteq k}a[i]\times b[j]\\
&=(\sum_{i\subseteq k}a[i])\times (\sum_{j\subseteq k}b[j])\\
&=A[k]\times B[k]
\end{align}
$$
也就是说快速莫比乌斯变换就是用来求集合的前缀和的,可以理解为它的本质是一个每一维都只有
$0/1$
的高位前缀和,也可以理解为按位分治,在这个求完之后像
$FFT$
一样对应位置相乘,然后再逆变换回去即可,逆变换就是加变成减,代码不变。
void FMT(ll f[],int l,int type)
{
for(int i = 0;i < l;++i)
{
for(int j = 0;j < (1 << l);++j)
{
if(((j >> i) & 1) == 0)f[j | (1 << i)] = f[j | (1 << i)] + type * f[j];
}
}
return;
}
快速沃尔什-哈达玛变换
用于计算位运算卷积。
先考虑异或卷积:
$$
c[k]=\sum_{i\text{ xor }j=k}a[i]\times b[j]
$$
有了
$FFT,NTT,FMT$
的经验,肯定是要构造一个变换,使得变换之后对应位置相乘再逆变换回去就是答案。
在这里设所有的向量都是从
$0$
到
$2^n-1$
。
定义:
$$
\begin{align}
A(x)+B(x)&=\{a[0]+b[0],a[1]+b[1],\dots,a[2^n-1]+b[2^n-1]\}\\
A(x)\times B(x)&=\{a[0]\times b[0],a[1]\times b[1],\dots,a[2^n-1]\times b[2^n-1]\}\\
A(x)\oplus B(x)&=C(x)\ \ C(x)就是我们要求的异或卷积\\
A_0(x)=\{a[0],&a[1],\dots,a[2^{n-1}-1]\},A_1(x)=\{a[2^{n-1}],a[2^{n-1}+1],\dots,a[2^n-1]\}
\end{align}
$$
那么我们定义变换(也叫
$FWT$
算子)
$tf$
:
$$
\begin{align}
tf(A)&=a_0,k=0\\
tf(A)&=(tf(A_0)+tf(A_1),tf(A_0)-tf(A_1))
\end{align}
$$
引理:
$$
tf(A+B)=tf(A)+tf(B)
$$
用数学归纳法证明:
$$
\begin{align}
tf(A+B)&=A+B=tf(A)+tf(B),k=0\\
tf(A+B)&=(tf(A_0+B_0)+tf(A_1+B_1),tf(A_0+B_0)-tf(A_1+B_1))\\
&=(tf(A_0)+tf(B_0)+tf(A_1)+tf(B_1),tf(A_0)+tf(B_0)-tf(A_1)-tf(B_1))\\
&=(tf(A_0)+tf(A_1),tf(A_0)-tf(A_1))+(tf(B_0)+tf(B_1),tf(B_0)-tf(B_1))\\
&=tf(A)+tf(B),k>0
\end{align}
$$
接下来就是要证明:
$$
tf(A)\times tf(B)=tf(C)
$$
还是要用数学归纳法,假设在
$k-1$
的情况成立:
$$
\begin{align}
tf(A)\times tf(B)&=(tf(A_0)+tf(A_1),tf(A_0)-tf(A_1))\times (tf(B_0)+tf(B_1),tf(B_0)-tf(B_1))\\
&=(tf(A_0)tf(B_0)+tf(A_1)tf(B_0)+tf(A_0)tf(B_1)+tf(A_1)tf(B_1))+\\
&\ \ \ \ \ (tf(A_0)tf(B_0)-tf(A_1)tf(B_0)-tf(A_0)tf(B_1)+tf(A_1)tf(B_1))\\
&=(tf(A_0\oplus B_0)+tf(A_1\oplus B_0)+tf(A_0\oplus B_1)+tf(A_1\oplus B_1))+\\
&\ \ \ \ \ (tf(A_0\oplus B_0)-tf(A_1\oplus B_0)-tf(A_0\oplus B_1)+tf(A_1\oplus B_1))\\
\\
tf(C)&=tf(A_0\oplus B_0+A_1\oplus B_1,A_0\oplus B_1+A_1\oplus B_0)\\
&=(tf(A_0\oplus B_0+A_1\oplus B_1)+tf(A_0\oplus B_1+A_1\oplus B_0),\\
&\ \ \ \ \ \ \ tf(A_0\oplus B_0+A_1\oplus B_1)-tf(A_0\oplus B_1+A_1\oplus B_0))\\
&=(tf(A_0\oplus B_0)+tf(A_1\oplus B_0)+tf(A_0\oplus B_1)+tf(A_1\oplus B_1))+\\
&\ \ \ \ \ (tf(A_0\oplus B_0)-tf(A_1\oplus B_0)-tf(A_0\oplus B_1)+tf(A_1\oplus B_1))\\
\end{align}
$$
得证。
在定义逆变换
$utf$
,我们只要让
$utf(tf(C))=C$
就可以了。
$$
utf(C)=(\frac{utf(C_0+C_1)}{2},\frac{utf(C_0-C_1)}{2})
$$
证明:
$$
\begin{align}
utf(tf(C))&=(\frac{utf(tf(C)_0+tf(C)_1)}{2},\frac{utf(tf(C)_0-tf(C)_1)}{2})\\
&=(\frac{utf(tf(C_0)+tf(C_1)+tf(C_0)-tf(C_1))}{2},\frac{utf(tf(C_0)+tf(C_1)-tf(C_0)+tf(C_1))}{2})\\
&=(\frac{utf(2tf(C_0))}{2},\frac{utf(2tf(C_1))}{2})\\
\because&\ tf(A)+tf(B)=tf(A+B)\\
utf(tf(C))&=(\frac{utf(tf(2C_0))}{2},\frac{utf(tf(2C_1))}{2})\\
&=(\frac{2C_0}{2},\frac{2C_1}{2})\\
&=(C_0,C_1)\\
&=C
\end{align}
$$
于是按照这个变换求解即可。
与卷积:
$tf(A)=(tf(A_0)+tf(A_1),tf(A_1)),utf(A)=(utf(A_0)-utf(A_1),utf(A_1))$
或卷积:
$tf(A)=(tf(A_0),tf(A_0)+tf(A_1)),utf(A)=(utf(A_0),utf(A_1)-utf(A_0))$
注意或卷积是
$utf(A_1)-utf(A_0)$
而不是
$utf(A_0)-utf(A_1)$
。
异或卷积的另一个重要性质:
$$
g[i]=\sum (-1)^{bitcount(i\text{ and }j)}f[j]
$$
#include<algorithm>
#include<iostream>
#include<cstdlib>
#include<cstdio>
#include<cmath>
#include<cctype>
#include<cstring>
using namespace std;
int n;
#define MAXN 18
typedef long long ll;
ll a[1 << MAXN],b[1 << MAXN];
ll res[1 << MAXN];
#define MOD 998244353
#define INV2 499122177
void FWT_or(ll f[],int l,int type)
{
for(int i = 2;i <= l;i = i << 1)
{
for(int j = 0;j < l;j += i)
{
for(int k = j;k < j + i / 2;++k)
{
ll u = f[k],t = f[k + i / 2];
if(type == 1)f[k + i / 2] = (u + t) % MOD;
else f[k + i / 2] = (t - u + MOD) % MOD;
}
}
}
return;
}
void FWT_and(ll f[],int l,int type)
{
for(int i = 2;i <= l;i = i << 1)
{
for(int j = 0;j < l;j += i)
{
for(int k = j;k < j + i / 2;++k)
{
ll u = f[k],t = f[k + i / 2];
if(type == 1)f[k] = (u + t) % MOD;
else f[k] = (u - t + MOD) % MOD;
}
}
}
return;
}
void FWT_xor(ll f[],int l,int type)
{
for(int i = 2;i <= l;i = i << 1)
{
for(int j = 0;j < l;j += i)
{
for(int k = j;k < j + i / 2;++k)
{
ll u = f[k],t = f[k + i / 2];
f[k] = (u + t) % MOD;
f[k + i / 2] = (u - t + MOD) % MOD;
if(type == -1)
{
f[k] = f[k] * INV2 % MOD;
f[k + i / 2] = f[k + i / 2] * INV2 % MOD;
}
}
}
}
return;
}
int main()
{
scanf("%d",&n);
for(int i = 0;i < (1 << n);++i)scanf("%d",&a[i]);
for(int i = 0;i < (1 << n);++i)scanf("%d",&b[i]);
FWT_or(a,1 << n,1);FWT_or(b,1 << n,1);
for(int i = 0;i < (1 << n);++i)res[i] = a[i] * b[i] % MOD;
FWT_or(res,1 << n,-1);FWT_or(a,1 << n,-1);FWT_or(b,1 << n,-1);
for(int i = 0;i < (1 << n);++i)printf("%lld ",res[i]);puts("");
FWT_and(a,1 << n,1);FWT_and(b,1 << n,1);
for(int i = 0;i < (1 << n);++i)res[i] = a[i] * b[i] % MOD;
FWT_and(res,1 << n,-1);FWT_and(a,1 << n,-1);FWT_and(b,1 << n,-1);
for(int i = 0;i < (1 << n);++i)printf("%lld ",res[i]);puts("");
FWT_xor(a,1 << n,1);FWT_xor(b,1 << n,1);
for(int i = 0;i < (1 << n);++i)res[i] = a[i] * b[i] % MOD;
FWT_xor(res,1 << n,-1);FWT_xor(a,1 << n,-1);FWT_xor(b,1 << n,-1);
for(int i = 0;i < (1 << n);++i)printf("%lld ",res[i]);puts("");
return 0;
}
拉格朗日插值法
根据常识,给定
$n+1$
个点的值可以唯一确定一个
$n$
次多项式,拉格朗日插值法就是用点值还原系数的一种方法。
定义
拉格朗日基本多项式
(也叫
插值基函数
)
$\ell(x)$
为:
$$
\ell_i(x)=\prod_{j=0,j\ne i}^n\frac{x-x_j}{x_i-x_j}=\frac{x-x_0}{x_i-x_0}\times\cdots\frac{x-x_{i-1}}{x_i-x_{i-1}}\times\frac{x-x_{i+1}}{x_i-x_{i+1}}\times\cdots\frac{x-x_n}{x_i-x_n}
$$
拉格朗日基本多项式的性质是只有当
$x=x_i$
时
$\ell_i(x)=1$
,
$x=x_j(j\ne i)$
时
$\ell_i(x)=0$
。
那么我们就可以利用这个多项式构造插值公式:
$$
L(x)=\sum_{i=0}^ny_i\ell_i(x)
$$
通过拉格朗日插值法可以
$O(n^2)$
的单点求值。
#include<algorithm>
#include<iostream>
#include<cstdlib>
#include<cstdio>
#include<cmath>
#include<cctype>
#include<cstring>
using namespace std;
int n;
typedef long long ll;
ll k;
#define MAXN 2010
ll x[MAXN],y[MAXN];
#define MOD 998244353
ll power(ll a,ll b)
{
ll res = 1;
while(b > 0)
{
if(b & 1)res = res * a % MOD;
a = a * a % MOD;
b = b >> 1;
}
return res;
}
ll inv(ll k){return power(k,MOD - 2);}
ll lagrange(ll k)
{
ll ans = 0;
for(int i = 1;i <= n;++i)
{
ll res = y[i];
for(int j = 1;j <= n;++j)
{
if(i == j)continue;
res = res * (k - x[j] + MOD) % MOD;
res = res * inv(x[i] - x[j] + MOD) % MOD;
}
ans = (ans + res) % MOD;
}
return ans;
}
int main()
{
scanf("%d%lld",&n,&k);
for(int i = 1;i <= n;++i)
{
scanf("%lld%lld",&x[i],&y[i]);
}
cout << lagrange(k) << endl;
return 0;
}
也可以
$O(n^2)$
的求原函数,具体做法是首先看拉格朗日插值的式子:
$$
f(x)=\sum_{i=1}^n\prod_{j=1,i\ne j}^n\frac{x-x_j}{x_i-x_j}y_i
$$
设
$w=\prod\limits_{j=1}^n(x-x_j)$
,那么:
$$
f(x)=\sum_{i=1}^n\frac w{x-x_i}a_i
$$
显然可以
$O(n^2)$
计算出所有的
$a_i$
,难的是分子部分,我们可以先计算出
$w$
,这个是
$O(n^2)$
的,然后每次做除法:
设
$F\times (x-x_i)=w$
,那么有:
$w[k]=F[k-1]-x_i\times F[k]$
,移一下项就是:
$$
F[k]=(F[k-1]-w[k])/x_i
$$
特殊的:
$w[0]=-F[0]\times x_i$
,因此一个个推过去就行了。
#include<algorithm>
#include<iostream>
#include<cstdlib>
#include<cstdio>
#include<cmath>
#include<cctype>
#include<cstring>
using namespace std;
typedef unsigned int uint;
int n;
#define MAXN 1700
uint val[MAXN],res[MAXN],val_[MAXN];
#define MOD 64123
uint power(uint a,int b)
{
uint res = 1;
while(b > 0)
{
if(b & 1)res = res * a % MOD;
a = a * a % MOD;
b = b >> 1;
}
return res;
}
uint inv(uint k){return power(k,MOD - 2);}
void calc(uint res[MAXN],uint val[MAXN],int n)
{
uint w[MAXN],a[MAXN];
w[0] = 1;
for(int i = 1;i <= n;++i)
{
a[i] = val[i];
for(int j = 1;j <= n;++j)
{
if(i == j)continue;
a[i] = a[i] * inv((i - j + MOD) % MOD) % MOD;
}
}
for(int i = 1;i <= n;++i)
{
for(int j = n;j >= 0;--j)w[j] = (w[j - 1] - i * w[j] % MOD + MOD) % MOD;
}
uint tmp[MAXN];
for(int i = 1;i <= n;++i)
{
tmp[0] = (-w[0] + MOD) % MOD * inv(i) % MOD;
for(int j = 1;j < n;++j)tmp[j] = (tmp[j - 1] - w[j] + MOD) % MOD * inv(i) % MOD;
for(int j = 0;j < n;++j)tmp[j] = tmp[j] * a[i] % MOD;
for(int j = 0;j < n;++j)res[j] = (res[j] + tmp[j]) % MOD;
}
return;
}
int main()
{
scanf("%d",&n);
for(int i = 1;i <= n;++i)scanf("%d",&val[i]);
calc(res,val,n);
for(int i = 0;i < n;++i)cout << res[i] << " ";cout << endl;
for(int i = 1;i <= n;++i)
{
uint ans = 0;
for(int j = 0,cur = 1;j < n;++j)
{
ans = (ans + cur * res[j] % MOD) % MOD;
cur = cur * i % MOD;
}
cout << ans << endl;
}
return 0;
}
 In tag:
In tag:
Copyright © 2020
wjh15101051
ღゝ◡╹)ノ♡
 Date: Thu Jun 14 21:07:01 CST 2018
Date: Thu Jun 14 21:07:01 CST 2018
 In Category:
In Category:

 Timeline
Timeline
 About
About
 Toolbox
Toolbox
 Friends
Friends